已知△ABC.(1)如图,AC⊥AB,点D为BC上一点,∠ABD=∠BAD,∠EAC=∠CAD,求证:AE∥BC.(2)如图,点P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,则∠ACB=______°,并证-数学-00教育-零零教育信息网
题文
已知△ABC.
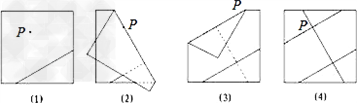
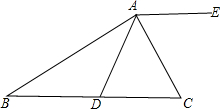
(1)如图,AC⊥AB,点D为BC上一点,∠ABD=∠BAD,∠EAC=∠CAD,
求证:AE∥BC.
(2)如图,点P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,则∠ACB=______°,并证明你的结论.

|
题型:解答题 难度:中档
答案

(1)证明:∵AC⊥AB,
∴∠ABC+∠ACB=90°,∠BAD+∠DAC=90°;
∵已知∠ABD=∠BAD,
∴∠ACB=∠DAC,
又∵已知∠EAC=∠CAD,
∴∠EAC=∠ACB,
∴AE∥BC.
(2)∠ACB=45°;
证明:连接PN,并经PN为直径作圆O,则正方形APMN为圆O的内接正方形;
∵NC⊥BC,∴点C在圆上,
∵PN为正方形的对角线,
∴∠ANP=45°,
∴∠ACB=45°(同弧对应的圆周角相等). |
据专家权威分析,试题“已知△ABC.(1)如图,AC⊥AB,点D为BC上一点,∠ABD=∠BAD,∠EAC=∠CAD..”主要考查你对 平行线的判定,正方形,正方形的性质,正方形的判定,正多边形和圆(内角,外角,中心角,边心距,边长,周长,面积的计算) 等考点的理解。关于这些考点的“档案”如下:
平行线的判定正方形,正方形的性质,正方形的判定正多边形和圆(内角,外角,中心角,边心距,边长,周长,面积的计算)
考点名称:平行线的判定
考点名称:正方形,正方形的性质,正方形的判定
考点名称:正多边形和圆(内角,外角,中心角,边心距,边长,周长,面积的计算)




 。(正方形边长为a,对角线长为b)
。(正方形边长为a,对角线长为b) 。
。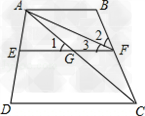

![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)