题文

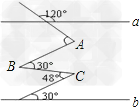
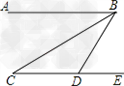
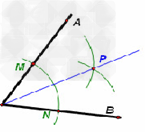
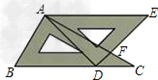
如图（1）所示，是一根木尺折断后的情形，你可能注意过，木尺折断后的断口一般是参差不齐的，那么你可深入考虑一下其中所包含的一类数学问题，我们不妨取名叫“木尺断口问题”． （1）如图（2）所示，已知AB∥CD，请问∠B，∠D，∠E有何关系并说明理由； （2）如图（3）所示，已知AB∥CD，请问∠B，∠E，∠D又有何关系并说明理由； （3）如图（4）所示，已知AB∥CD．请问∠E+∠G与∠B+∠F+∠D有何关系并说明理由．

题型：解答题  难度：中档

答案

（1）过E作EM∥AB，根据平行线的传递性，则EM∥CD， ∵EM∥AB∥CD， ∴∠MEB=∠B，∠MED=∠D， ∴∠B+∠D=∠E； （2）∵EM∥AB∥CD， ∴∠MEB+∠B=180°，∠MED+∠D=180°， ∴∠B+∠E+∠D=360°； （3）分别过E，F，G作AB的平行线，充分运用平行线的性质，得∠E+∠G=∠B+∠F+∠D．

据专家权威分析，试题“如图（1）所示，是一根木尺折断后的情形，你可能注意过，木尺折断后..”主要考查你对  平行线的性质，平行线的公理  等考点的理解。关于这些考点的“档案”如下：

平行线的性质，平行线的公理

考点名称：平行线的性质，平行线的公理

• 平行公理：过直线外一点有且只有一条直线与已知直线平行。
  推论（平行线的传递性）：平行同一直线的两直线平行。
  ∵a∥c，c ∥b
  ∴a∥b。

  平行线的性质：
  1. 两条平行被第三条直线所截，同位角相等。
  简单说成：两直线平行，同位角相等。
  2. 两条平行线被第三条直线所截，内错角相等。
  简单说成：两直线平行，内错角相等。
  3 . 两条平行线被第三条直线所截，同旁内角互补。
  简单说成：两直线平行，同旁内角互补。

• 平行线的性质公理注意：
  ①注意条件“经过直线外一点”，若经过直线上一点作已知直线的平行线，就与已知直线重合了；
  ②平行公理体现了平行线的存在性和唯一性；
  ③平行公理的推论体现了平行线的传递性。
  ④在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论。这是平行线特有的性质。不要一提同位角或内错角就认为他们相等，一提同旁内角就认为互补，若没有两直线平行的条件，他们是不成立的。