如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,(1)△ABC与△DBC的面积相等吗?为什么?(2)若S△AOB=21cm2,求S△COD;(3)若S△AOD=10cm2,且BO:OD=2:1,求S△ABD.-数学
题文
| 如图,四边形ABCD中,AD∥BC,AC与BD相交于点O, (1)△ABC与△DBC的面积相等吗?为什么? (2)若S△AOB=21cm2,求S△COD; (3)若S△AOD=10cm2,且BO:OD=2:1,求S△ABD. 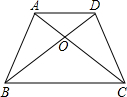 |
答案
| (1))△ABC与△DBC的面积相等,理由是: ∵AD∥BC, ∴△ABC的边BC上的高和△DBC边BC上的高相等,设此高为h, ∴△ABC的面积是
∵BC=BC, ∴△ABC与△DBC的面积相等; (2)∵S△ABC=S△DBC, ∴S△ABC-S△OBC=S△DBC-S△OBC, ∴S△AOB=S△DOC=21cm2, 即S△COD=21cm2; (3)∵BO:OD=2:1, ∴BD=3OD, ∵△AOD的边OD上的高和△ABD的边BD上的高相等,设此高为a, ∵S△AOD=
∴S△ABD.=
|
据专家权威分析,试题“如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,(1)△ABC与△DBC的面..”主要考查你对 平行线之间的距离 等考点的理解。关于这些考点的“档案”如下:
平行线之间的距离
考点名称:平行线之间的距离
- 两条平行线之间的距离:
是指从两条平行直线中的一条直线上的一点作另一条直线的垂线段的长;
注:
①能表示两条平行线之间的距离的线段与这两条平行线都垂直;
②平行线的位置确定之后,它们之间的距离是定值,它不随垂线段位置的改变而改变;
③平行线间的距离处处相等。 三种距离定义:
1.两点间的距离——连接两点的线段的长度;
2.点到直线的距离——直线外一点到这条直线的垂线段的长度;
3.两平行线的距离——两天平行线中,一条直线上的点到另一条直线的垂线段长度。两直线间的距离公式:
设两条直线方程为
Ax+By+C1=0
Ax+By+C2=0
则其距离公式为|C1-C2|/√(A2+B2)
推导:两平行直线间的距离就是从一条直线上任一点到另一条直线的距离,设点P(a,b)在直线Ax+By+C1=0上,
则满足Aa+Bb+C1=0,即Ab+Bb=-C1,由点到直线距离公式,P到直线Ax+By+C2=0距离为
d=|Aa+Bb+C2|/√(A2+B2)=|-C1+C2|/√(A2+B2)
=|C1-C2|/√(A2+B2)
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |