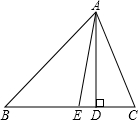
在小学学习中,我们已经知道三角形的三个角之和等于180°,如图,在三角形ABC中,∠C=70°,∠B=38°,AE是∠BAC的平分线,AD⊥BC于D.(1)求∠DAE的度数;(2)判定AD是∠EAC的平分线吗?-七年级数学
角平分线线定理:
定理1:在角平分线上的任意一点到这个角的两边距离相等。
逆定理:在一个角的内部(包括顶点),且到这个角的两边距离相等的点在这个角的角平分线上。
定理2:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例,
如:在△ABC中,BD平分∠ABC,则AD:DC=AB:BC
注:定理2的逆命题也成立。
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等!(即内心)。
定理1:在角平分线上的任意一点到这个角的两边距离相等。
逆定理:在一个角的内部(包括顶点),且到这个角的两边距离相等的点在这个角的角平分线上。
定理2:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例,
如:在△ABC中,BD平分∠ABC,则AD:DC=AB:BC
注:定理2的逆命题也成立。
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等!(即内心)。
1.垂直平分线垂直且平分其所在线段。
2.垂直平分线上任意一点,到线段两端点的距离相等。
3.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等。
垂直平分线的逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
<?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />
方法一:
1、取线段的中点。
2、分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线。得到一个交点。
3、连接这两个交点。
原理:等腰三角形的高垂直等分底边。
方法二:
1、分别以线段的两个端点为圆心,以大于线段的二分之一长度为半径画弧线,得到两个交点。原理:圆的半径处处相等。
2、连接这两个交点。原理:两点成一线。
垂直平分线的概念:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)
考点名称:三角形中位线定理
- 三角形中位线定义:
连接三角形两边中点的线段叫做三角形的中位线。一个三角形共有三条中位线。
三角形中位线定理:
三角形的中位线平行于第三边,并且等于它的一半。
如图已知△ABC中,D,E分别是AB,AC两边中点。
则DE平行于BC且等于BC/2 - 三角形中位线逆定理:

逆定理一:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是三角形的中位线。
如图DE//BC,DE=BC/2,则D是AB的中点,E是AC的中点。
逆定理二:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
如图D是AB的中点,DE//BC,则E是AC的中点,DE=BC/2 - 区分三角形的中位线和中线:
三角形的中位线是连结三角形两边中点的线段;
三角形的中线是连结一个顶点和它的对边中点的线段。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:已知△ABC的三个内角度数之比为3:4:5,则此三角形是()三角形。[]A.锐角B.钝角C.直角D.不能确定-七年级数学
下一篇:一个三角形三个内角度数的比是2:3:4,这个三角形是()三角形.[]A.锐角B.直角C.钝角D.等边-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |