如图,PB和PC是△ABC的两条外角平分线.①求证:∠BPC=90°-12∠BAC.②根据第①问的结论猜想:三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?-数学
题文
| 如图,PB和PC是△ABC的两条外角平分线. ①求证:∠BPC=90°-
②根据第①问的结论猜想:三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?  |
答案
| ①证明:∵PB和PC是△ABC的两条外角平分线, ∴∠P=180°-(∠PBC+∠PCB) =180°-
=180°-
=180°-
=90°-
②根据①的结论,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角, 三个角都是锐角的三角形是锐角三角形,故该三角形是锐角三角形. |
据专家权威分析,试题“如图,PB和PC是△ABC的两条外角平分线.①求证:∠BPC=90°-12∠BAC.②根..”主要考查你对 三角形的外角性质 等考点的理解。关于这些考点的“档案”如下:
三角形的外角性质
考点名称:三角形的外角性质
- 三角形的外角:
三角形的一条边的延长线和另一条相邻的边组成的角,叫做三角形的外角。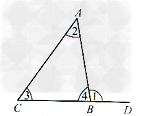
∠1是三角形的外角。 三角形的外角特征:
①顶点在三角形的一个顶点上,如∠ACD的顶点C是△ABC的一个顶点;
②一条边是三角形的一边,如∠ACD的一条边AC正好是△ABC的一条边;
③另一条边是三角形某条边的延长线如∠ACD的边CD是△ABC的BC边的延长线。
性质:
①. 三角形的外角与它相邻的内角互补。
②. 三角形的一个外角等于和它不相邻的两个内角的和。
③. 三角形的一个外角大于任何一个和它不相邻的内角。
④. 三角形的外角和等于360°。
设三角形ABC 则三个外角和=(A+B)+(A+C)+(B+C)=360度。
定理:三角形的一个外角等于不相邻的两个内角和。
定理:三角形的三个内角和为180度。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![如图所示,∠A=32°,∠B=40°,∠C=38°,则∠DFE等于[]A.120°B.115°C.110°D.105°-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/156/2020-01-10/7c436f23df3e9f98a22284a1fcd641ee.png)

![如图,∠BDC=98°,∠C=38°,∠B=23°,则∠A=[]A.61°B.60°C.37°D.39°-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/156/2020-01-10/404c6d1a54a659dac2fd8b20e6760ca1.gif)
