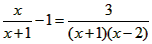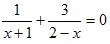(1)先化简,再求代数式a-ba÷(a-2ab-b2a)的值,其中a=3tan30°+1,b=2cos45°.(2)解方程:xx-1-2x-2x-1=0.-数学
题文
(1)先化简,再求代数式
(2)解方程:
|
答案
(1)原式=
当a=3tan30°+1=
(2)方程的两边同乘x(x-1),得 x2-(2x-2)(x-1)-x(x-1)=0, 解得x1=2,x2=
检验:把x1=2代入x(x-1)=2≠0. ∴x1=2是原方程的解; 把x2=
∴x2=
∴x1=2,x2=
|
据专家权威分析,试题“(1)先化简,再求代数式a-ba÷(a-2ab-b2a)的值,其中a=3tan30°+1,..”主要考查你对 解分式方程,分式的加减乘除混合运算及分式的化简,特殊角三角函数值 等考点的理解。关于这些考点的“档案”如下:
解分式方程分式的加减乘除混合运算及分式的化简特殊角三角函数值
考点名称:解分式方程
- 解法:
解分式方程的基本思想是把分式方程转化为整式方程,其一般步骤是:
(1)去分母:分式方程两边同乘以方程中各分母的最简公分母,把分式方程转化为整式方程。
(最简公分母:①系数取最小公倍数②出现的字母取最高次幂③出现的因式取最高次幂)
(2)解方程:解整式方程,得到方程的根;
(3)验根:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;
否则,这个解不是原分式方程的解,是原分式方程的增根。
如果分式本身约分了,也要带进去检验。
在列分式方程解应用题时,不仅要检验所得解的是否满足方程式,还要检验是否符合题意。
一般的,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为零,因此要将整式方程的解代入最简公分母,如果最简公分母的值不为零,则是方程的解.
注意:
(1)注意去分母时,不要漏乘整式项。
(2)増根是分式方程去分母后化成的整式方程的根,但不是原分式方程的根。
(3)増根使最简公分母等于0。
分式方程的特殊解法:
换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法。 解分式方程的基本思路是将分式方程化为整式方程,具体做法是“去分母”,即方程两边同乘最简公分母,这也是解分式方程的一般思路和做法。
解分式方程注意:
①解分式方程的基本思想是把分式方程转化为整式方程,通过解整式方程进一步求得分式方程的解;
②用分式方程中的最简公分母同乘方程的两边,从而约去分母,但要注意用最简公分母乘方程两边各项时,切勿漏项;
③解分式方程可能产生使分式方程无意义的情况,那么检验就是解分式方程的必要步骤。
考点名称:分式的加减乘除混合运算及分式的化简
- 分式的加减乘除混合运算:
分式的混合运算应先乘方,再乘除,最后算加减,有括号的先算括号内的。也可以把除法转化为乘法,再运用乘法运算。
分式的化简:借助分式的基本性质,应用换元法、整体代入法等,通过约分和通分来达到简化分式的目的。 分式的混合运算:
在解答分式的乘除法混合运算时,注意两点,就可以了:
注意运算的顺序:按照从左到右的顺序依次计算;
注意分式乘除法法则的灵活应用。
考点名称:特殊角三角函数值
- 特殊角三角函数值表:

- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

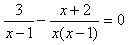
![若有増根,则m的值是[]A.-2B.2C.3D.-3-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/85/2019-04-09/47ddc84666083f5bc2f5081659719228.gif)