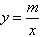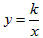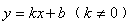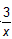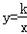如图，已知△OAB中，AB=AO=20，点B的坐标为（-32，0）。（1）求过点A的反比例函数的解析式；（2）若点C在坐标轴上，且∠CAO=90°，试求点C的坐标。-八年级数学-00教育-零零教育信息网

如图，已知△OAB中，AB=AO=20，点B的坐标为（-32，0）。（1）求过点A的反比例函数的解析式；（2）若点C在坐标轴上，且∠CAO=90°，试求点C的坐标。-八年级数学

首页 > 考试 > 数学 > 初中数学 > 求反比例函数的解析式及反比例函数的应用/2019-04-13 / 加入收藏 / 阅读 [打印]

题文

如图，已知△OAB中，AB=AO=20 ，点B的坐标为（-32 ，0）。
（1）求过点A 的反比例函数的解析式；
（2）若点C在坐标轴上，且∠CAO=90°，试求点C的坐标。

题型：解答题难度：中档

答案

解：（1）作AH⊥BO于H，
∵AB=A，
∴BH=OH
∵B 的坐标为（-32，0 ），
∴OB=32，
∴OH=16，又OA=20
∴
∴A（-16，12）
∴过点A的反比例函数的解析式为：；
（2）①当点C在x轴上时（如图甲）
设OC=x，则HC=x-16
在Rt△AHC中，∠AHC=90°
∴AC²=AH²+HC²，
在Rt△OAC中，∠CAO=90°，
∴AC²=OC²-OA²
∴AH²+HC²=OC²-OA²，
∴12²+（x-16）²=x²-20²
解得：x=25
∴C（-25，0）
②延长CA交y轴与点C'（如图乙）
则∠C'AO= 90°
设直线CA的解析式为y=kx+b，
∵C（-25，0），A（-16，12）
∴
解得：，
∴C′，
综上所述：点C的坐标为（- 25，0）或，
②的另解，当点C在y轴上时（如图丙）
过点A作AD⊥OC轴于点D，则OD=12，
AD=16设OC=x，则CD=x-12
同理由勾股定理可得：
AC²=AD²+CD²=OC²-OA²
∴16²+（x-12）²=x²-20²解得：
∴
综上所述：点C的坐标为（-25，0）或。

甲

乙

丙

据专家权威分析，试题“如图，已知△OAB中，AB=AO=20，点B的坐标为（-32，0）。（1）求过点A的..”主要考查你对求反比例函数的解析式及反比例函数的应用，勾股定理等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用勾股定理

考点名称：求反比例函数的解析式及反比例函数的应用

反比例函数解析式的确定方法：
由于在反比例函数关系式：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

反比例函数的应用：
建立函数模型，解决实际问题。
用待定系数法求反比例函数关系式的一般步骤是：
①设所求的反比例函数为：y= (k≠0)；
②根据已知条件（自变量与函数的对应值）列出含k的方程；
③由代人法解待定系数k的值；
④把k值代人函数关系式y= 中。

反比例函数应用一般步骤：
①审题；
②求出反比例函数的关系式；
③求出问题的答案，作答。

考点名称：勾股定理

勾股定理:
直角三角形两直角边(即“勾”，“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说，如果直角三角形的两直角边长分别为a，b，斜边长为c，那么。
勾股定理只适用于直角三角形，应用于解决直角三角形中的线段求值问题。
定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现，从而深刻揭示了数与量的区别，即所谓“无理数"与有理数的差别，这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程，也是最早得出完整解答的不定方程，它一方面引导到各式各样的不定方程，包括著名的费尔马大定理，另一方面也为不定方程的解题程序树立了一个范式。
勾股定理的应用：
数学
从勾股定理出发开平方、开立方、求圆周率等，运用勾股定理数学家还发现了无理数。
勾股定理在几何学中的实际应用非常广泛，较早的应用案例有《九章算术》中的一题：“今有池，芳一丈，薛生其中央，出水一尺，引薛赴岸，适与岸齐，问水深几何？答曰："一十二尺"。

生活
勾股定理在生活中的应用也较广泛，举例说明如下：
1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例，最佳的屏幕尺寸主要取决于使用空间的面积，从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕，也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点：
第一，屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6；
第二，屏幕到第一排座位的距离应大于2倍屏幕的高度；
第三，屏幕底部应离观众席所在地面最少122厘米。
屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3，教育幕为正方形。如一个72英寸的屏幕，根据勾股定理，很快就能得出屏幕的宽为1.5m，高为1.1m。
2、2005年珠峰高度复测行动。
测量珠峰的一种方法是传统的经典测量方法，就是把高程引到珠峰脚下，当精确高程传递至珠峰脚下的6个峰顶交会测量点时，通过在峰顶竖立的测量觇标，运用“勾股定理”的基本原理测定珠峰高程，配合水准测量、三角测量、导线测量等方式，获得的数据进行重力、大气等多方面改正计算，最终得到珠峰高程的有效数据。
通俗来说，就是分三步走：
第一步，先在珠峰脚下选定较容易的、能够架设水准仪器的测量点，先把这些点的精确高程确定下来；
第二步，在珠峰峰顶架起觇标，运用三角几何学中“勾股定理”的基本原理，推算出珠峰峰顶相对于这几个点的高程差；
第三步，获得的高程数据要进行重力、大气等多方面的改正计算，最终确定珠峰高程测量的有效数据。