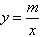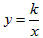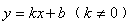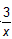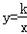题文

如图所示是某一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用的时间t（h）之间 的函数关系图象． （1）请你根据图象提供的信息求出此蓄水池的蓄水量； （2）求出此函数的解析式； （3）若要6h排完水池中的水，那么每小时的排水量应该是多少？ （4）如果每小时排水量不超过5 000m3，那么水池中的水至少要多少小时排完？

题型：解答题  难度：中档

答案

（1）设V= k t ． ∵点（12，4000）在此函数图象上， ∴蓄水量为12×4000=48000m3； （2）∵点（12，4000）在此函数图象上， ∴4000= k 12 ， k=48000， ∴此函数的解析式V= 48000 t ； （3）当t=6时，V= 48000 6 =8000m3； ∴每小时的排水量应该是8000m3； （4）∵V≤5000， ∴ 48000 t ≤5000， ∴t≥9.6． ∴水池中的水至少要9.6小时排完．

据专家权威分析，试题“如图所示是某一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。