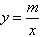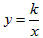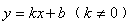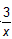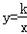题文

某蓄水池的排水管每小时排水6m3，12小时可将满池水全部排空． （1）该蓄水池的容积是多少？ （2）现计划增加排水管，使每小时的排水量达到Q （m3），那么将满池水排空所需的时间t（时）将如何变化？并写出t与Q之间的关系式； （3）如果计划在8小时内将满池水排空，那么每小时的排水量至少为多少立方米？ （4）已知排水管的最大排水量为每小时12m3，那么最少多长时间可将满池水全部排空？

题型：解答题  难度：中档

答案

（1）容积为6×12=72（m3） （2）将满池水排空所需的时间t（时）将减少， t与Q之间的关系式是t= 72 Q （3）当t=8时，t= 72 Q =8∴Q=9∴每小时排水量至少为9米3． （4）当Q=12时，t= 72 12 =6（小时） ∴最少6小时可将满池水全部排空．

据专家权威分析，试题“某蓄水池的排水管每小时排水6m3，12小时可将满池水全部排空．（1）该..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。