照样子,写出数量关系.例:实际比计划增产110.数量关系:计划产量+计划产量×110=实际产量,或者计划产量×(1+110)=实际产量.(1)爸爸的工资收入比妈妈多27.数量关系:______(2)桃-数学
 =(x,y)叫做向量
=(x,y)叫做向量 的坐标表示。
的坐标表示。基底在向量中的应用:
(l)用基底表示出相关向量来解决向量问题是常用的方法之一.
(2)在平面中选择基底主要有以下几个特点:①不共线;②有公共起点;③其长度及两两夹角已知.(3)用基底表示向量,就是利用向量的加法和减法对有关向量进行分解。
用已知向量表示未知向量:
用已知向量表示未知向量,一定要结合图像,可从以下角度如手:
(1)要用基向量意识,把有关向量尽量统一到基向量上来;
(2)把要表示的向量标在封闭的图形中,表示为其它向量的和或差的形式,进而寻找这些向量与基向量的关系;
(3)用基向量表示一个向量时,如果此向量的起点是从基底的公共点出发的,一般考虑用加法,否则用减法,如果此向量与一个易求向量共线,可用数乘。
考点名称:用数量积表示两个向量的夹角
用数量积表示两个向量的夹角:
设
 都是非零向量,
都是非零向量, ,θ是
,θ是 与
与 的夹角,根据向量数量积的定义及坐标表示可得
的夹角,根据向量数量积的定义及坐标表示可得 。
。向量数量积问题中方法提炼:
(1)平面向量的数量积的运算有两种形式,一是依据定义来计算,二是利用坐标来计算,具体应用哪种形式应根据已知条件的特征来选择;
(2)平面向量数量积的计算类似于多项式的运算,解题中要注意多项式运算方法的运用;
(3)平面向量数量积的计算中要注意平面向量基本定理的应用,选择合适的基底,以简化运算
(4)向量的数量积是一个数而不是一个向量。
考点名称:向量模的计算
向量的模:
设
 ,则有向线段
,则有向线段 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: ,则
,则  。
。向量模的坐标表示:
(1)若
 ,则
,则 ;
;
(2)若 ,那么
,那么 。
。求向量的模:
求向量的模主要是利用公式
 来解。
来解。
考点名称:平面向量的应用
平面向量在几何、物理中的应用
1、向量在平面几何中的应用:
(1)证明线段相等平行,常运用向量加法的三角形法则、平行四边形法则,有时也用到向量减法的定义;
(2)证明线段平行,三角形相似,判断两直线(或线段)是否平行,常运用到向量共线的条件;
(3)证明垂直问题,常用向量垂直的充要条件;
1、向量在三角函数中的应用:
(1)以向量为载体研究三角函数中最值、单调性、周期等三角函数问题;
(2)通过向量的线性运算及数量积、共线来解决三角形中形状的判断、边角的大小与关系。
2、向量在物理学中的应用:
由于力、速度是向量,它们的分解与合成与向量的加法相类似,可以用向量方法来解决,力做的功就是向量中数量积的一种体现。
3、向量在解析几何中的应用:
(1)以向量为工具研究平面解析几何中的坐标、性质、长度等问题;
(2)以向量知识为工具研究解析几何中常见的轨迹与方程问题。平面向量在几何、物理中的应用
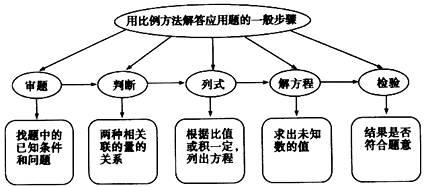
1、用向量解决几何问题的步骤:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如:距离,夹角等;
(3)把运算结果“翻译”成几何关系。
2、用向量中的有关知识研究物理中的相关问题,步骤如下:
(1)问题的转化,即把物理问题转化为数学问题;
(2)模型的建立,即建立以向量为主题的数学模型;
(3)求出数学模型的有关解;
(4)将问题的答案转化为相关的物理问题。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![甲数的等于乙数的,乙数是甲数的3倍。[]-六年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/fenshuchengfajiyingyong/2019-05-23/c6b939e62f7ec2b30def8961a0e156c1.gif)


