仔细推敲,认真辨析。(对的打“√”,错的打“×”)(1)扇形统计图能清楚地表示出数量的增减变化。[](2)一组数据中可能不会有众数,也可能有几个众数。[](3)小明身高1.4米,肯定能-六年级数学
题文
| 仔细推敲,认真辨析。(对的打“√”,错的打“×”) | |||||||||||
|
答案
| (1)×;(2)√;(3)×;(4)①×;②√ |
据专家权威分析,试题“仔细推敲,认真辨析。(对的打“√”,错的打“×”)(1)扇形统计图能清楚..”主要考查你对 统计(众数),统计(平均数),折线统计图,可能性,概率 等考点的理解。关于这些考点的“档案”如下:
统计(众数)统计(平均数)折线统计图可能性,概率
考点名称:统计(众数)
- 众数:
是在一组数据中,出现次数最多的数据,是一组数据中的原数据,而不是相应的次数。
一组数据可以有多个众数,也可以没有众数。
如数据2、3、-1、2、1、3中,2、3都出现了两次,它们都是这组数据中的众数。
数据1、2、4、5、8、9中各个数据都出现一次,所以这组数据不存在众数。
考点名称:统计(平均数)
- 定义:
平均数是指在一组数据中所有数据之和再除以数据的个数。
意义:
平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。 - 平均数的特点:
平均数比一组数据中最大的数小,比最小的数大。 - 方法点拨:
平均数=总数量÷总分数
考点名称:折线统计图
- 折线统计图:
用一个单位长度表示一定数量,用折线的上升或下降表示数量的多少和增减变化。容易看出数量的增减变化情况。 - 折现统计图制作步骤:
1.标题:根据统计表所反映的内容,在正上方写上统计图的名称;
2.画出横、纵轴:先画纵轴,后画横轴,横、纵轴都要有单位,按纸面的大小来确定用一定单位表示一定的数量;
3.描点、连线:根据数量的多少,在纵、横轴的恰当位置描出各点,然后把各点用线段顺序连接起来。
考点名称:可能性,概率
可能性:
是指事物发生的概率,是包含在事物之中并预示着事物发展趋势的量化指标。有些事件的发生是确定的,有些是不确定的。用“可能”、“不可能”“一定”等表达事物发生的情况。
常见方法有:抛骰子、摸球、转盘。
概率:
又称或然率、机会率或机率、可能性,是数学概率论的基本概念,是一个在0到1之间的实数,是对随机事件发生的可能性的度量。随机事件:
有些事件在一定的条件下可能发生,也可能不发生,结果不确定。例如,购买彩票能否 中奖,开出的列车能否正点到达。明年今天是否下雨等待,我们称之为随机事件。
我们用随机事件的“概率”来表示随机事件发生可能性大小:概率是0到1之间的一个数,概率随机事件发生的可能性大。
在小学阶段我们只计算最简单的一些随机事件的概率,这种计算方法以“等可能性”为基础。在有些情况下,虽然有些事情的结果是不确定的(随机性的),但是由于某种“对称性”,不同的基本结果发生的可能性是相同的,这时,我们说这些基本结果是等可能的,从而确定相关事件的概率。例如:
投一枚均匀硬币,“出现正面”“出现反面”这两种基本结果是等可能的,所以“出现正面”和“出现反面”的概率都是1/2;
投一枚色子(骰子),“出现1点”“出现2点”......“出现6点”这六种基本情况是等可能的,其概率是1/6 。
对于随机事件,我们关心的是事件发生的可能性。
事件发生的可能性大小是可以比较的,所以人们常说一件事情“不可能”""不大可能”“很可能”“非常可能”“绝对可能”......这些说法反应可能性大小的不同程度。
射击时,“射中十环”的可能性比“射中九环”的可能性小;
一分钟投篮,“投中15个”比“投中10个”的可能性小
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

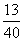
把5米长的绳子平均分成7份,每份是这根绳子长的。[](3)大于小于的分数只有。[](4)表面积相等-五年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/tongjizhongshu/2019-05-18/b7431e1e590e34d71ea7665415372a07.gif)



