如果有9个外观一样的彩球,其中有一个是次品,次品比正品略轻一些.用天平,不用砝码,最少需要称几次能保证找出次品?是3次,4次,还是2次?方法之一:,把9个彩球分成3组,每组-数学
题文
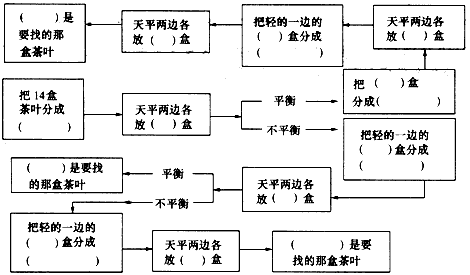
| 如果有9个外观一样的彩球,其中有一个是次品,次品比正品略轻一些.用天平,不用砝码,最少需要称几次能保证找出次品?是3次,4次,还是2次? 方法之一:,把9个彩球分成3组,每组3个.先在天平两边分别放3个球,如果平衡,次品在没称的3个球中;如果不平衡,次品在较轻的一边.再把含有次品的3个球中的2个放在天平两边,如果平衡,次品是没称的那个;如果不平衡,次品是较轻的那个.这样只需要称2次. 方法之二:先在天平两边各放4个彩球.想一想一共需要称几次? 数量分别是27个、81个外观一样的彩球,其中有一个是次品,次品比正品略轻一些.用天平,不用砝码,最少需称几次能保证找出次品?请你设计一个方案. |
答案
| 答:运用方法二需要称3次: 第一次:在天平两边各放4个彩球,若平衡,则未取那个彩球就为次品,若不平衡;第二次:把天平秤较高端的4个彩球,平均分成两份,每份2个,分别放在天平秤两端;第三次:把天平秤较高端的2个彩球,分别放在天平秤两端,较高端的彩球即为次品. 若有27个彩球,需要称3次; 把27个彩球平均分成3份,每份9个,第一次:任取两份分别放在天平秤两端,若天平秤平衡,则次品在未取的那9个彩球中,若不平衡;第二次:把天平秤较高端的9个彩球平均分成3份,每份3个,任取2份,分别放在天平秤两端,若平衡,则次品在未取的那3个彩球中,若不平衡;第三次:把较高端的3个彩球,任取2个,分别放在天平秤两端,较高端彩球即为次品. 若有81个彩球,需要称4次; 把81个彩球平均分成3份,每份27个,第一次:任取两份分别放在天平秤两端,若天平秤平衡,则次品在未取的那27个彩球中,若不平衡;再按照27个彩球找其中一个次品的方法即可解答. |
据专家权威分析,试题“如果有9个外观一样的彩球,其中有一个是次品,次品比正品略轻一些..”主要考查你对 找次品 等考点的理解。关于这些考点的“档案”如下:
找次品
考点名称:找次品
- 找次品:
根据天平的平衡原理对托盘两边的物品进行比较。把待测物品分成三份;
要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:56个零件中有一个次品,比其它零件稍轻一点,用天平至少称______次,就能保证找到这个次品.-数学
下一篇:有50枚金币,其中一枚是假币,而外观和真的一样.只是比真币轻一点,你能用一架没有砝码的天平称4次把假币找出来吗?-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |