判断(对的打“√”,错的打“×”。)(1)用“四舍五入”法取近似值,保留两位小数约等于4.60的三位小数,最大的是4.599。[](2)盒子里放着4个球,上面分别写着2,3,5,7。任意摸一球-六年级数学
题文
判断(对的打“√”,错的打“×”。)
|
答案
| (1)×;(2)×;(3)√;(4)×;(5)× |
据专家权威分析,试题“判断(对的打“√”,错的打“×”。)(1)用“四舍五入”法取近似值,保留两..”主要考查你对 正方体的体积,求小数的近似值,正方体的表面积,百分数的计算,百分数的应用题,正比例的意义,反比例的意义 等考点的理解。关于这些考点的“档案”如下:
正方体的体积求小数的近似值正方体的表面积百分数的计算,百分数的应用题正比例的意义,反比例的意义
考点名称:正方体的体积
- 正方体的体积公式:
正方体的体积=棱长×棱长×棱长;V=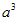 。
。
正方体的体积=底面积×高;V=sh。
考点名称:求小数的近似值
- 求近似数:
是根据需要用“四舍五入法”保留一定的小数位数。 - 方法点拨:
求近似数时:保留整数,表示精确到个位;保留一位小数,表示精确到十分位;保留两位小数,表示精确到百分位……
如:豆豆身高0.984米
求:1、保留两位小数: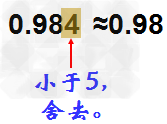
如果保留两位小数,就要第三位数省略。
2、保留一位小数:

如果保留一位小数,就要把第二、三位小数省略。
在表示近似数时,小数末尾的0不能去掉。
3、保留整数部分: ≈1
≈1
省略个位后面的尾数
考点名称:正方体的表面积
- 正方体的表面积公式:
正方体的表面积=棱长×棱长×6;S=6 。
。
考点名称:百分数的计算,百分数的应用题
- 常见的百分数的计算方法:

- 百分数应用题关系式:
利息的计算公式:利息=本金×利率×时间。
百分率:例:发芽率=发芽种子数÷试验种子数×100%
利率=利息÷本金×100%
折数=现价÷原价
成数=实际收成÷计划收成
税率=应纳税额÷总收入×100%
利润=售出价-成本,利润率=利润÷成本×100%=(售出价÷成本-1)×100%
折扣=实际售价÷原售价×100%(折扣<1)
浓度问题:
溶质的重量+溶剂的重量=溶液的重量;
溶质的重量÷溶液的重量×100%=浓度;
溶液的重量×浓度=溶质的重量;
溶质的重量÷浓度=溶液的重量。
考点名称:正比例的意义,反比例的意义
正比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线;
用字母表示为如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用以下关系式表示: =k(一定);
=k(一定);
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变.正比例和反比例
反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;
如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定)。- 反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
成反比例的量:
前提:两种相关的量(乘法关系)
要求:一个量变化,另一个量也随着变化,并且,这两个量中相对应的两个数的乘积一定。
结论:这两个量就叫做反比例的量,它们的关系叫做反比例关系。 正比例和反比例关系:
相同点:
①正比例和反比例都含有三个数量,在这三个数量中,均有一个定量、两个变量。
②在正、反比例的两个变量中,均是一个量变化,另一个量也随之变化。并且变化方式均属于扩大(乘以一个数)或缩小(除以一个数)若干倍的变化。
不同点:
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线;反比例是曲线。
③公式不同:正比例是( =k(一定)),反比例是(xy=k(一定))。
=k(一定)),反比例是(xy=k(一定))。
④规律不同:正比例是一个数缩小,另一个数也缩小,一个数扩大,另一个数也扩大;反比例是一个数缩小,另一个数就扩大,一个数扩大另一个数就缩小。- 判断两种量成正比例、反比例或不成比例的方法:
(1)找出两种相关联的量。
(2)根据两种相关联的量之间的关系列出数量关系式。
(3)如果两种量中相对应的两个数的比值(也就是商)一定,就是成正比例的量;若积一定,就是反比例的量。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![一个水箱从里面量长100cm,宽80cm,高50cm,装满水后,水箱的容积是[]A.400000LB.4000LC.400L-五年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/zhengfangtidetiji/2019-04-24/70bb5b953cd8754e6037b12b88a946bc.png)
![表面积相等的两个正方体,它们的体积也一定相等。[]-六年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/zhengfangtidetiji/2019-04-24/f43f861b182a61fdadcf29d20f9118a6.png)
![棱长为2分米的水箱(正方体形)的体积和容积[]A.体积大B.容积大C.一样大D.无法比较-五年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/zhengfangtidetiji/2019-04-24/820ff15d304b59d1ae81faa87422452b.png)