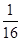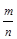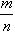如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同-数学
题文
| 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标). (1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率. (2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为
 |


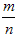 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。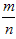 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1; 。(正方形边长为a,对角线长为b)
。(正方形边长为a,对角线长为b) ;点P(x,y)在第二象限
;点P(x,y)在第二象限
 ;点P(x,y)在第四象限
;点P(x,y)在第四象限
 y=0,x为任意实数
y=0,x为任意实数  x=0,y为任意实数
x=0,y为任意实数  x,y同时为零,即点P坐标为(0,0)。
x,y同时为零,即点P坐标为(0,0)。  。
。