题文

下列叙述正确的是（　　） A．调查一批新型节能灯泡的使用寿命，采用全面调查 B．商场经理要了解哪种衬衫型号最畅销，他最关注的是衬衫型号的中位数 C．为了了解我市参加中考的12000名学生的视力情况，抽查了500名学生的视力进行统计分析，每名学生是总体的一个个体 D．某种彩票中奖概率是1%，买1张这种彩票可能会中奖．

题型：单选题  难度：中档

答案

A、调查一批新型节能灯泡的使用寿命，具有破坏性，只能采用抽样调查，故本选项错误； B、商场经理要了解哪种衬衫型号最畅销，他应该最关注衬衫型号的众数，故本选项错误； C、每名学生的视力情况是总体的一个个体，故本选项错误； D、概率表示发生的机会的大小，机会小也有可能发生，所以买1张这种彩票有可能会中奖，故本选项正确． 故选D．

据专家权威分析，试题“下列叙述正确的是（）A．调查一批新型节能灯泡的使用寿命，采用全面..”主要考查你对  概率的意义，全面调查和抽样调查 ，总体、个体、样本、样本容量  等考点的理解。关于这些考点的“档案”如下：

概率的意义全面调查和抽样调查 总体、个体、样本、样本容量

考点名称：概率的意义

• 概率的意义：
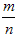  一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
  事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
  事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
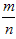  注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
  （2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
  （3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
  （4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

考点名称：全面调查和抽样调查

• 全面调查：
  就是对需要调查的对象进行逐个调查。这种方法所得资料较为全面可靠，但调查花费的人力、物力、财力较多，且调查时间较长，不适合一般企业的要求。全面调查只在产品销售范围很窄或用户很少的情况下可以采用。对品种多、产量大、销售范围广的产品，就不适用全面调查，而可以采用抽样调查。
  抽样调查：
  是从需要调查对象的总体中，抽取若干个个体即样本进行调查，并根据调查的情况推断总体的特征的一种调查方法。
  抽样调查可以把调查对象集中在少数样本上，并获得与全面调查相近的结果。这是一种较经济的调查方法，因而被广泛采用。抽样调查是从研究对象的总体中抽取一部分个体作为样本进行调查，据此推断有关总体的数字特征。

• 调查好处与特点:
  1.全面调查：对需要调查的对象进行逐个调查。
  好处：所得资料较为全面可靠。
  特点：调查花费的人力、物力、财力较多，且调查时间较长，全面调查只在样本很少的情况下适合采用。

  2.抽样调查：是一种非全面调查，它是从全部调查研究对象中，抽选一部分单位进行调查，并据以对全部调查研究对象作出估计和推断的一种调查方法。
  好处：耗费的人力，物力，财力少，大量节约调查时间。
  特点：
  1、按随机原则抽选样本。
  2、总体中每一个单位都有一定的概率被抽中。
  3、可以用一定的概率来保证将误差控制在规定的范围之内。
  4、适合样本数量较多的情况下采用。

• 全面调查和抽样调查关系:
  全面调查和抽样调查是按调查对象范围不同划分的调查方式。
  全面调查是对调查对象中的所有单位全部加以调查，通过基层单位按照一定的报表填报要求进行逐一登记、逐级上报、层层汇总，最后取得调查结果的一种调查方式，如人口普查、经济普查等。
  抽样调查是一种非全面调查，它是从研究的总体中按随机原则抽取部分样本单位进行调查，并根据样本单位的调查结果来推断总体，以达到认识总体的一种统计调查方式。
  
  抽样调查用样本指标代表总体指标不可避免会产生误差，抽样推断虽然会有抽样误差(不包括登记误差和系统性误差)，但只要严格遵守随机原则，所选的样本结构与总体结构相同，或者两者分布一致，就可以运用数学公式计算抽样误差。随机抽样产生的误差，只要确定其具体的数量界限，可以通过抽样程序设计加以控制。因此抽样调查的结果是有可靠的科学依据的。
  
  抽样调查与全面调查有着相辅相成的关系。在实际运用中，没有必要进行全面调查和不可能进行全面调查时宜采用抽样调查。
  抽样调查的优点:
  一是由于只从总体中抽取一部分样本进行调查，工作量小，所以比全面调查节省人力、物力、财力，比较经济；
  二是可以及时取得调查资料，提高数据的时效性；
  三是数据质量有保证，由于抽样调查一般是自上而下组织调查，直接派员深入实际抽取样本并推断总体，可以减少人为因素干扰，只要取样、推断方法科学，均有利于提高数据的质量；
  第四，调查方法灵活，如实际工作中使用较多的问卷调查、入户调查、电话调查等，适应面广，特别适于对点多面广的总体作调查。

考点名称：总体、个体、样本、样本容量

• 掌握总体、个体、样本，样本容量的概念，能正确区分总体、个体、样本、样本容量
  总体、个体、样本、样本容量，这四个概念之间其实有其内在联系，
  总体：我们把所要考察的对象的全体叫做总体；
  个体：把组成总体的每一个考察对象叫做个体；
  样本：从总体中取出的一部分个体叫做这个总体的一个样本；
  样本容量：一个样本包含的个体的数量叫做这个样本的容量。
  我们在区分这四个概念时，首先找出考察的对象，从而找出总体、个体，再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量。