题文

某种类型的图钉被抛起后触地，针尖朝上的概率是 2 3 ，下列说法正确的是（　　） A．如果抛3次，那么就有2次针尖朝上 B．如果抛3000次，那么就有2000次针尖朝上 C．如果抛3000次，那么就有2000次左右针尖朝上 D．图钉被抛起触地后，并不能确认针尖是朝上还是朝下，所以说概率是多少，没有意义

题型：单选题  难度：偏易

答案

A、B、是偶然事件，不会一定发生，故选项错误； C、实际频率与数学概率接近，正确； D、概率是多次实验得到一个和实际频率接近的值，有可取性，故选项错误． 故选C．

据专家权威分析，试题“某种类型的图钉被抛起后触地，针尖朝上的概率是23，下列说法正确..”主要考查你对  概率的意义  等考点的理解。关于这些考点的“档案”如下：

概率的意义

考点名称：概率的意义

• 概率的意义：
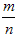  一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
  事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
  事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
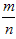  注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
  （2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
  （3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
  （4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。