题文

下列说法中，错误的是（　　） A．三角形的三条高都在三角形内 B．成轴对称的两个图形一定全等 C．若必然事件发生的概率记为P，则有P=1 D．直角三角形有两条高与直角边重合

题型：单选题  难度：偏易

答案

A、钝角三角形有两条高在三角形外部，一条高在三角形内部，故这种说法是错误的，本选项正确； B、两个图形成轴对称，这两个图形是全等图形，故这种说法是正确的，本选项错误； C、必然事件就是一定发生的事件，必然事件发生的概率是1，故这种说法是正确的，本选项错误； D、直角三角形有两条高与直角边重合，这种说法是正确的，故本选项错误． 故选A．

据专家权威分析，试题“下列说法中，错误的是（）A．三角形的三条高都在三角形内B．成轴对称..”主要考查你对  概率的意义，三角形的中线，角平分线，高线，垂直平分线，轴对称  等考点的理解。关于这些考点的“档案”如下：

概率的意义三角形的中线，角平分线，高线，垂直平分线轴对称

考点名称：概率的意义

• 概率的意义：
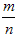  一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
  事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
  事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
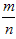  注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
  （2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
  （3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
  （4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

考点名称：三角形的中线，角平分线，高线，垂直平分线

• 三角形的中线：
  在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。由于三角形有三条边，所以一个三角形有三条中线。且三条中线交于一点。这点称为三角形的重心。
  每条三角形中线分得的两个三角形面积相等。
  角平分线：
  三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。
  三角形的角平分线不是角的平分线，是线段。角的平分线是射线。
  高线：
  从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。
  线段的垂直平分线：
  经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线。
  

  <?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />注意：要证明一条线为一个线段的垂直平分线，应证明两个点到这条线段的距离相等且这两个点都在要求证的直线上才可以证明
  巧计方法：点到线段两端距离相等。

• 三角形中线性质定理：
  1、三角形的三条中线都在三角形内。<?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />

  2、三角形的三条中线长：

  ma=(1/2)√2b²+2c² -a² ；

  mb=(1/2)√2c² +2a² -b²  ；

  mc=(1/2)√2a² +2b² -c²  。

  (ma,mb,mc分别为角A,B,C所对的中线长）

  3、三角形的三条中线交于一点，该点叫做三角形的重心。

  4、直角三角形斜边上的中线等于斜边的一半。

  5.三角形中线组成的三角形面积等于这个三角形面积的3/4.

  定理内容：三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。

   

  角平分线线定理：
  定理1：在角平分线上的任意一点到这个角的两边距离相等。
  逆定理：在一个角的内部（包括顶点），且到这个角的两边距离相等的点在这个角的角平分线上。
  定理2：三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例，
  如：在△ABC中，BD平分∠ABC，则AD：DC=AB：BC
  注：定理2的逆命题也成立。
  三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。

   

  垂直平分线的性质：
  1.垂直平分线垂直且平分其所在线段。  
  2.垂直平分线上任意一点，到线段两端点的距离相等。  
  3.三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的距离相等。  
  垂直平分线的逆定理：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

• <?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />垂直平分线的尺规作法：
  方法一：
  1、取线段的中点。
  2、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线。得到一个交点。
  3、连接这两个交点。
  原理：等腰三角形的高垂直等分底边。
  方法二：
  1、分别以线段的两个端点为圆心，以大于线段的二分之一长度为半径画弧线，得到两个交点。原理：圆的半径处处相等。
  2、连接这两个交点。原理：两点成一线。
  垂直平分线的概念：经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）

考点名称：轴对称

• 轴对称的定义：
  把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合 ，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点,叫做对称点。轴对称和轴对称图形的特性是相同的，对应点到对称轴的距离都是相等的。

• 轴对称的性质：
  （1）对应点所连的线段被对称轴垂直平分；
  （2）对应线段相等，对应角相等；
  （3）关于某直线对称的两个图形是全等图形。

• 轴对称的判定：
  如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。
  这样就得到了以下性质：
  1.如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。
  2.类似地，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。
  3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。　
  4.对称轴是到线段两端距离相等的点的集合。

  轴对称作用:
  可以通过对称轴的一边从而画出另一边。
  可以通过画对称轴得出的两个图形全等。
  扩展到轴对称的应用以及函数图像的意义。

  轴对称的应用:
  关于平面直角坐标系的X,Y对称意义
  如果在坐标系中，点A与点B关于直线X对称，那么点A的横坐标不变，纵坐标为相反数。
  相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。

  关于二次函数图像的对称轴公式(也叫做轴对称公式 )
  设二次函数的解析式是 y=ax²+bx+c
  则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b²)/4a

  在几何证题、解题时，如果是轴对称图形，则经常要添设对称轴以便充分利用轴对称图形的性质。
  譬如，等腰三角形经常添设顶角平分线；
  矩形和等腰梯形问题经常添设对边中点连线和两底中点连线；
  正方形，菱形问题经常添设对角线等等。
  另外，如果遇到的图形不是轴对称图形，则常选择某直线为对称轴，补添为轴对称图形，
  或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中。