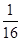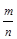端午节吃粽子是中华民族的传统习俗.又快到农历五月初五端午节了,小明奶奶包了6个粽子,其中有3个是枣豆馅的,有2个是鲜肉馅的,有1个是咸蛋黄馅的(这些粽子除馅料不同外其他-数学
题文
| 端午节吃粽子是中华民族的传统习俗.又快到农历五月初五端午节了,小明奶奶包了6个粽子,其中有3个是枣豆馅的,有2个是鲜肉馅的,有1个是咸蛋黄馅的(这些粽子除馅料不同外其他外观均相同.小明随手拿了两只来吃. (1)求小明第一个就吃到了喜欢的鲜肉馅粽子的概率. (2)求小明所吃两只粽子馅料相同的概率. (3)若在吃粽子之前,小明准备用一枚均匀的正六面体骰子进行吃粽子的模拟试验,规定:掷得点数1,2,3向上代表吃枣豆馅的,点数4,5向上代表吃鲜肉馅的,点数6向上代表吃咸蛋黄馅的,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是枣豆馅的概率.你认为这样模拟正确吗?试说明理由. |
答案
(1)小明第一个就吃到了喜欢的鲜肉馅粽子的概率是
(2)设枣豆馅的、鲜肉馅的、咸蛋黄馅的分别为A、B、C,列表得:
∴小明所吃两只粽子馅料相同的概率是
(3)不正确.概率问题需要做多次试验,才可近似求得. |
据专家权威分析,试题“端午节吃粽子是中华民族的传统习俗.又快到农历五月初五端午节了,..”主要考查你对 概率的意义,列举法求概率,二次函数的最大值和最小值 等考点的理解。关于这些考点的“档案”如下:
概率的意义列举法求概率二次函数的最大值和最小值
考点名称:概率的意义
- 概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率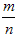 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤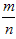 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
考点名称:列举法求概率
- 可能条件下概率的意义:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
 。
。
等可能条件下概率的特征:
(1)对于每一次试验中所有可能出现的结果都是有限的;
(2)每一个结果出现的可能性相等。 - 概率的计算方法:
(1)列举法(列表或画树状图),
(2)公式法;
列表法或树状图这两种举例法,都可以帮助我们不重不漏的列出所以可能的结果。
列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)列表法的应用场合
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
(2)运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
考点名称:二次函数的最大值和最小值
- 二次函数的最值:
1.如果自变量的取值范围是全体实数,则当a>0时,抛物线开口向上,有最低点,那么函数在 处取得最小值y最小值=
处取得最小值y最小值= ;
;
当a<0时,抛物线开口向下,有最高点,即当 时,函数取得最大值,y最大值=
时,函数取得最大值,y最大值= 。
。
也即是:如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当 时,
时, 。
。
2.如果自变量的取值范围是 ,那么,首先要看
,那么,首先要看 是否在自变量取值范围
是否在自变量取值范围 内,若在此范围内,则当x=
内,若在此范围内,则当x= 时,
时, ;若不在此范围内,则需要考虑函数在
;若不在此范围内,则需要考虑函数在 范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时,
范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2 时, ,当x=x1 时
,当x=x1 时 ;如果在此范围内,y随x的增大而减小,则当x=x1时,
;如果在此范围内,y随x的增大而减小,则当x=x1时, ,当x=x2时
,当x=x2时 。
。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:在中央电视台第2套《购物街》栏目中,有一个精彩刺激的游戏--幸运大转盘,其规则如下:①游戏工具是一个可绕轴心自由转动的圆形转盘,转盘按圆心角均匀划分为20等分,并在其边缘-数学
下一篇:在课外活动课上,某小组有4名女生,2名男生,随机指定一人为组长,恰好是女生的概率是______.-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |