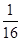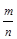濠电姷鏁告慨鐢割敊閺嶎厼绐楁俊銈呮噺閺咁亪姊绘担鍓插悢闁哄鐏濋‖鍫ユ煕濡ゅ懍鎲鹃柡宀€鍠栧鑽も偓鐢登规俊浠嬫⒑缁嬪灝顒㈤柛銊ユ健瀵鈽夊⿰鍛澑闂佸搫娲ㄩ崑娑欑濮椻偓濮婂搫效閸パ冾瀷闂佺ǹ顑嗛幐鑽ょ矚鏉堛劎绡€闁搞儴鍩栭弲顒勬⒑閹稿海绠撻悗姘煎弮瀹曟劙鏁愰崶鈺冿紳婵炶揪绲肩划娆撳传閾忓湱纾奸悹鍥ㄥ絻椤忣亞绱掗崒娑樻诞闁轰礁鍊块幊鐐哄Ψ瑜忚倴闂傚倷绶氬ḿ褑鍔归梺閫炲苯澧撮柡浣稿暣瀹曟帒鈽夊顒€绠哄┑锛勫亼閸婃洜鎹㈤幇顔瑰亾濮橆剙妲婚崡閬嶆煙闂傚鍔嶉柣鎾存礋閺屾洝绠涢妷褏锛熼梺鍛婄憿閸嬫捇姊绘担渚敯婵炲懏娲栫叅闁哄稁鍙忕紞鏍ㄧ節闂堟侗鍎忛崬顖炴⒑闂堟稓绠冲┑顔挎珪缁旂喖寮撮姀鈾€鎷虹紓浣割儐鐎笛冿耿閺夎¥鈧帒顫濋褎鐤侀悗瑙勬礃濞叉牠锝炲⿰鍫濈劦妞ゆ巻鍋撴い顐㈢箲缁绘繂顫濋鍌︾床闂備線娼ч悧鍡涘箠韫囨稒鍊堕柡鍥╁剱濞撳鏌曢崼婵嗘殭闁诲浚浜弻娑㈠Ω閵夈儺鏆㈢紓渚囧枛椤戝懘顢橀崗鐓庣窞濠电姳鑳堕悙濠囨⒒娴e憡鍟炴繛璇х畵瀹曟垿宕卞☉杈ㄦ櫓閻庡厜鍋撻柛鏇ㄥ厴閹风粯绻涢幘纾嬪婵炲眰鍊曢锝囨崉閵娧咃紳閻庡箍鍎扮粈浣圭閸撗呯=闁稿本鐟ч崝宥嗘叏婵犲偆鐓肩€规洑鍗冲浠嬵敇閻愬鈧剟鎮楅獮鍨姎妞わ缚鍗冲畷鎴﹀礋椤栨稓鍘介梺鐟邦嚟閸嬪秶绱撳鑸电厽闁挎繂妫楅埢鏇熸叏婵犲倹鎯堥悡銈夋偣娴h姤鐝柟鐧哥秮濮婅櫣绮欏▎鎯у壉闂佸憡姊瑰ú鐔煎春閵忋倕绫嶉柛顐g箘閸樻悂姊洪崨濠佺繁闁哥姵鐗犲畷婊堫敋閳ь剙顫忓ú顏勭闁圭粯甯婄花鑲╃磽娴g瓔鍤欑紒澶嬫綑瀹撳嫰姊绘笟鍥у缂佸鏁婚幃陇绠涘☉娆戝幈闂佹枼鏅涢崰姘枔閺冨牊鐓冪憸婊堝礈濠靛缍栧鑸靛姇閻ら箖鏌涢锝嗙闁稿鍔欓弻褑绠涢敐鍛盎閻庢鍠栧ḿ锟犲蓟閿濆棙鍎熸い鏍ㄧ矌鏍¢梻浣告憸婵數鏁垾宕囨殾闁硅揪绠戠粻濠氭倵濞戞顏堫敁閹剧粯鐓熼柣鏂挎憸閹冲啴鎮楀顒佸櫣妞ゎ偅绻冨ḿ蹇涘Ω閵夛妇鈧箖姊绘担铏瑰笡妞ゃ劌鎳橀幃褔宕卞☉娆戝帓濠电姴锕ら幊鎰婵傜ǹ绾ч柛顐g☉婵¤法绱掗悩闈涗户闁逞屽墲椤煤閳哄啰绀婂ù锝呮憸閺嗭箑鈹戦崒婧撶懓鏁梻渚€娼х换鎺撴叏閾忣偆鐝堕柡鍥╁枔缁犻箖寮堕崼婵嗏挃闁告帊鍗抽弻鐔烘嫚瑜忕弧鈧悗瑙勬礃閸ㄤ絻鐏掗梺绋跨箳閸樠囧几閹达附鈷戠紓浣癸供濞堟棃鏌eΔ鈧Λ娑氬垝椤撱垹绠抽柟鍨暞椤旀棃姊虹紒妯哄闁宦板妼閻i浠︾憴锝嗘杸闂佹枼鏅涢崯顖滀焊閿旈敮鍋撶憴鍕閻㈩垱甯¢崺鐐哄箣閿曗偓楠炪垽鏌嶇悰鈥充壕闂佺懓顕崗妯侯潖缂佹ɑ濯撮柛娑橈工閺嗗牓鏌i姀鈺佺仯闁稿鍋ゅ鑼崉娴f洘妫冨畷銊╊敊閻撳骸顥掑┑鐘垫暩閸嬫稑螞濞嗘挸绠伴柛婵勫劜閸忔粓鏌嶈閸撴瑩鍩為幋鐐茬疇闂佺ǹ锕ュú婊堝焵椤掍礁鍤柛鎾跺枎閻i鎲撮崟顒€顎撶紓渚囧灡濞叉﹢锝炲澶嬧拺闁荤喐婢橀埛鏃€銇勯幒鎾跺弨鐎殿喓鍔庣槐鎺懳熼崷顓犵暰闁诲海鎳撴竟濠囧窗閺嶃劍娅犻柟缁㈠枟閻撴稑霉閿濆懏鎲搁懖鏍ㄧ箾鐎电ǹ顎撶紒鐘虫崌楠炴劖绻濋崘銊х獮閻庡厜鍋撻悗锝庡墰椤︽澘鈹戦悩鍨毄闁稿鍋ゅ畷褰掑醇閺囩偟顔囩紓浣割儐閿涙洖煤椤忓嫀褍顭跨捄鐚村姛妞ゆ柨妫欑换娑㈠级閹存繃鍊┑鐐插悑閻熲晛鐣烽敐鍡欑瘈闁搞儯鍔庨崢顏呯節閵忥絾纭鹃柣妤€妫濋崺鈧い鎺嶇贰濞堟ḿ绱掗鑺ヮ棃鐎规洖銈稿鎾偄閸濆嫬濡囬梻鍌欒兌绾泛危閸涙潙鍌ㄩ柣锝呭閸嬫挸顫濋悙顒€顏�
一只箱子里原有3个球,其中2个白球,1个红球,它们除颜色外均相同.(1)从箱子中任意摸出两个球,用树状图或列表法列举出所有可能并求两次摸出球的都是白球的概率.(2)若从箱子-九年级数学
题文
| 一只箱子里原有3个球,其中2个白球,1个红球,它们除颜色外均相同. (1)从箱子中任意摸出两个球,用树状图或列表法列举出所有可能并求两次摸出球的都是白球的概率. (2)若从箱子中任意摸出一个球是红球的概率为 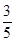 ,则需要再加入几个红球?. ,则需要再加入几个红球?. |
答案
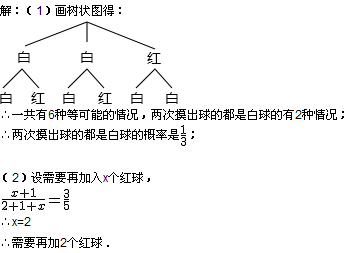 |
| 略 |
据专家权威分析,试题“一只箱子里原有3个球,其中2个白球,1个红球,它们除颜色外均相同..”主要考查你对 概率的意义,随机事件,必然事件,列举法求概率 等考点的理解。关于这些考点的“档案”如下:
概率的意义随机事件必然事件列举法求概率
考点名称:概率的意义
- 概率的意义:
一般地,在大量重复试验中,如果事件A发生的频率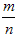 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:必然事件的概率为1,不可能事件的概率为0,随机事件A的概率为0<P(A)<1。
注:(1)在n试验中,事件A发生的频率m满足0≤m≤n,所以0≤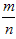 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;
(2)P(A)=0表示事件A是不可能发生的事件,P(A)=1表示事件A是必然发生的事件;
(3)概率越大,表示事件发生的可能性越大;概率越小,表示事件发生的可能性越小;
(4)人们通常对随机事件进行大量的反复试验来研究概率,一般大量试验事件发生的频率可作为概率的估计值。
考点名称:随机事件
随机事件:
事件可分为确定事件和不确定事件,不确定事件又称为随机事件。
在一定条件下,可能发生也可能不发生的事件。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。
事件的概率:随机事件A的概率为0<P(A)<1。- 随机事件特点:
1.可以在相同的条件下重复进行;
2.每个试验的可能结果不止一个,并且能事先预测试验的所有可能结果;
3.进行一次试验之前不能确定哪一个结果会出现。
注意:
①随机事件发生与否,事先是不能确定的;
②必然事件发生的机会是1;不可能事件发生的机会是0;随机事件发生的机会在0-1之间。
③要判断一个事件是必然事件、随机事件、还是不可能事件,要从定义出发。
考点名称:必然事件
- 必然事件:
事件可分为确定事件和不确定事件,确定事件可分为必然事件和不可能事件。
在一定的条件下,一定发生的事件。
事件和概率的表示方法:一般地,事件用英文大写字母A,B,C,…,表示事件A的概率p,可记为P(A)=P。必然事件的概率为1。
考点名称:列举法求概率
- 可能条件下概率的意义:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=
 。
。
等可能条件下概率的特征:
(1)对于每一次试验中所有可能出现的结果都是有限的;
(2)每一个结果出现的可能性相等。 - 概率的计算方法:
(1)列举法(列表或画树状图),
(2)公式法;
列表法或树状图这两种举例法,都可以帮助我们不重不漏的列出所以可能的结果。
列表法
(1)定义:用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
(2)列表法的应用场合
当一次试验要设计两个因素, 并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
树状图法
(1)定义:通过列树状图列出某事件的所有可能的结果,求出其概率的方法叫做树状图法。
(2)运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:四张完全相同的卡片上,分别画上圆、矩形、等边三角形、等腰三角形。现从中随机抽取2张,全部是中心对称图形的概率是_________-七年级数学
下一篇:将两枚同样大小的硬币放在桌上,固定其中一枚,而另一枚则沿着其边缘滚动一周,这时滚动的硬币滚动了.-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |