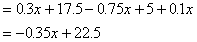甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,所给的枚数等于乙,丙原来各有的邮票数;然后依同样的游戏规则再由乙送给甲,丙现有的邮票数,最后由丙送给-数学
题文
| 甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,所给的枚数等于乙,丙原来各有的邮票数;然后依同样的游戏规则再由乙送给甲,丙现有的邮票数,最后由丙送给甲,乙现有的邮票数.互相送完后,每人恰好各有64枚.你能知道他们原来各有邮票多少枚吗?说出你的思考过程. |
答案
设甲原有邮票x枚,乙原有邮票y枚,丙原有邮票z枚.
即
③-②得 2z-y=8 ④, ②+①得 y-z=24 ⑤, ④+⑤得 z=32, 将z代入⑤得 y=56, 将y、z代入①得 x=104, 答:甲原有邮票104枚,乙原有邮票56枚,丙原有邮票32枚. |
据专家权威分析,试题“甲,乙,丙三人各有邮票若干枚,要求互相赠送.先由甲送给乙,丙,..”主要考查你对 三元(及三元以上)一次方程(组)的应用 等考点的理解。关于这些考点的“档案”如下:
三元(及三元以上)一次方程(组)的应用
考点名称:三元(及三元以上)一次方程(组)的应用
- 三元一次方程组的应用:求待定系数的值,列方程组解应用题等。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:某专卖店有A、B、C三种袜子,若买A种4双、B种7双、C种1双共需26元;若买A种5双、B种9双,C种1双共需32元,问A、B、C三种袜子各买1双共需多少元?-数学
下一篇:现有A、B、C三种型号的产品出售,若售A3件,B2件,C1件,共得315元;若售A1件,B2件,C3件,共得285元.问售出A、B、C各一件共得多少元?-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |