下列命题中正确的是()A.平分弦的直径垂直于弦B.圆心角的度数等于圆周角度数的2倍C.对角线相等且互相垂直的四边形是菱形D.到两条平行线距离相等的点的轨迹,是和这两条平行线-数学
题文
下列命题中正确的是( )
|
答案
| A、此弦不能是直径,故此选项错误; B、必须是同弧或等弧所对的圆心角和圆周角之间才有2倍的关系,故此选项错误; C、对角线互相垂直平分的四边形是菱形,故此选项错误; D、根据两条平行线间的距离的概念,故此选项正确. 故选D. |
据专家权威分析,试题“下列命题中正确的是()A.平分弦的直径垂直于弦B.圆心角的度数等于..”主要考查你对 平行线的判定,菱形,菱形的性质,菱形的判定,垂直于直径的弦,圆心角,圆周角,弧和弦 等考点的理解。关于这些考点的“档案”如下:
平行线的判定菱形,菱形的性质,菱形的判定垂直于直径的弦圆心角,圆周角,弧和弦
考点名称:平行线的判定
- 平行线的概念:
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥,如“AB∥CD”,读作“AB平行于CD”。
注意:
①平行线是无限延伸的,无论怎样延伸也不相交。
②当遇到线段、射线平行时,指的是线段、射线所在的直线平行。 平行线的判定平行线的判定公理:
(1)两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简称:同位角相等,两直线平行。
(2)两条直线被第三条直线所截,如果内错角相等,那么两直线平行。简称:内错角相等,两直线平行。
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。简称:同旁内角互补,两直线平行。
还有下面的判定方法:
(1)平行于同一条直线的两直线平行。
(2)垂直于同一条直线的两直线平行。
(3)平行线的定义。判定方法的逆应用:
在同一平面内,两直线不相交,即平行。
两条直线平行于一条直线,则三条不重合的直线互相平行。
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
6a⊥c,b⊥c则a∥b。
考点名称:菱形,菱形的性质,菱形的判定
- 菱形的定义:
在一个平面内,有一组邻边相等的平行四边形是菱形。 菱形的性质:
①菱形具有平行四边形的一切性质;
②菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角;
③菱形的四条边都相等;
④菱形既是轴对称图形(两条对称轴分别是其两条对角线所在的直线),也是中心对称图形(对称中心是其重心,即两对角线的交点);
⑤在有一个角是60°角的菱形中,较短的对角线等于边长,较长的对角线是较短的对角线的根号3倍。菱形的判定:
在同一平面内,
(1)定义:有一组邻边相等的平行四边形是菱形
(2)定理1:四边都相等的四边形是菱形
(3)定理2:对角线互相垂直的平行四边形是菱形
菱形是在平行四边形的前提下定义的,首先它是平行四边形,而且是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定方法。
菱形的面积:S菱形=底边长×高=两条对角线乘积的一半。
考点名称:垂直于直径的弦
垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
注:
(1)定理中的直径过圆心即可,可以是直径、半径、过圆心的直线或线段;
(2)此定理是证明等线段、等角、垂直的主要依据,同时也为圆的有关计算提供了方法和依据。
垂径定理的推论:
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论一:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧
推论二:弦的垂直平分线经过圆心,并且平分这条弦所对的弧
推论三:平分弦所对的一条弧的直径垂直平分这条弦,并且平分这条弦所对的另一条弧
推论四:在同圆或者等圆中,两条平行弦所夹的弧相等
(证明时的理论依据就是上面的五条定理)
但是在做不需要写证明过程的题目中,可以用下面的方法进行判断:一条直线,在下列5条中只要具备其中任意两条作为条件,就可以推出其他三条结论
1.平分弦所对的优弧
2.平分弦所对的劣弧
(前两条合起来就是:平分弦所对的两条弧)
3.平分弦 (不是直径)
4.垂直于弦
5.经过圆心
考点名称:圆心角,圆周角,弧和弦
圆的定义:
在同一平面内,到定点的距离等于定长的点的集合叫做圆。这个定点叫做圆的圆心。图形一周的长度,就是圆的周长。
弧:
圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示以A,B为端点的弧记作“ ”,读作“圆弧AB”或“弧AB”。
”,读作“圆弧AB”或“弧AB”。
优弧:大于半圆的弧(多用三个字母表示);
劣弧:小于半圆的弧(多用两个字母表示)
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
弧、弦、弦心距、圆心角之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角:
顶点在圆心的角叫做圆心角。
圆周角:
顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。圆心角特征识别:
①顶点是圆心;
②两条边都与圆周相交。计算公式:
①L(弧长)=n/180Xπr(n为圆心角度数,以下同);
②S(扇形面积) = n/360Xπr2;
③扇形圆心角n=(180L)/(πr)(度)。
④K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。圆心角定理:
圆心角的度数等于它所对的弧的度数。
理解:(定义)
(1)等弧对等圆心角
(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.
(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.
(4)圆心角的度数和它们对的弧的度数相等.
推论:
在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等与圆周角关系:
在同圆或等圆中,同弧或同弦所对的圆周角等于二分之一的圆心角。
定理证明:分三种情况讨论,始终做直径COD,利用等腰三角形等腰底角相等,外角等于两内角之和来证明。
圆周角定理推论:
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

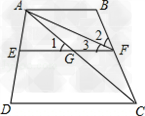

![如图,下列说法中,正确的是[]A.因为∠A+∠D=180°,所以AD∥BCB.因为∠C+∠D=180°,所以AB∥CDC.因为∠A+∠D=180°,所以AB∥CDD.因为∠A+∠C=180°,所以AB∥CD-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/150/2020-01-07/6a9802b7a026a5297753da5eca5ae992.png)