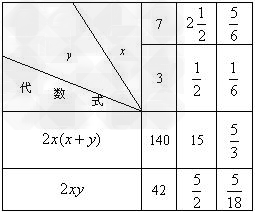
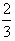某校举行庆祝十六大的文娱汇演,评出一等奖5个,二等奖10个,三等奖15个.学校决定给获奖的学生发奖品,同一等次的奖品相同,并且只能从下表所列物品中选取一件:品名小提琴运-数学
题文
某校举行庆祝十六大的文娱汇演,评出一等奖5个,二等奖10个,三等奖15个.学校决定给获奖的学生发奖品,同一等次的奖品相同,并且只能从下表所列物品中选取一件:
(2)学校要求一等奖的奖品单价是二等奖奖品单价的5倍,二等奖的奖品单价是三等奖奖品单价的4倍;在总费用不超过1000元的前提下,有几种购买方案?花费最多的一种方案需要多少钱? |

![设“●”“”“”表示三种不同的物体,现用天平称了两次,情况如图所示,那么“”“”“●”这三种物体按质量从大到小的排列顺序为[]A.●B.●C.●D.●-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/56/2019-03-20/f0186856bab1d1cd1e7bef49f699b7ce.png)
![设表示三种不同的物体,用天平比较它们质量的大小,情况如下图,那么这三种物体按质量从大到小的顺序为[]A.B.C.D.-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/56/2019-03-20/34f4bcd0031e61e2cff1523504101314.png)