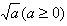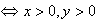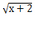题文

一水池内有水90立方米，设全池水排尽的时间为y分钟，每分钟的排水量为x立方米， 排水时间的范围是9≤y≤15 （1）求y关于x的函数解析式，并指出每分钟排水量x的取值范围； （2）在坐标系中画出此函数的图象； （3）根据图象求当每分钟排水量为9立方米时，排水需多少分钟？当排水时间为10分钟时，每分钟的排水量是多少立方米？

题型：解答题  难度：中档

答案

（1）∵每小时排水量×排水时间=蓄水池的容积， ∴y= 90 x ， ∵排水时间的范围是9≤y≤15 ∴6≤x≤10； （2） （3）令x=9，解得y=10， 令y=10求得x=9， ∴当每分钟排水量为9立方米时，排水需10分钟；当排水时间为10分钟时，每分钟的排水量是9立方米．

据专家权威分析，试题“一水池内有水90立方米，设全池水排尽的时间为y分钟，每分钟的排水..”主要考查你对  函数值，函数的图像，求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

函数值函数的图像求反比例函数的解析式及反比例函数的应用

考点名称：函数值

• 定义：
  函数的值是指自变量在其取值范围内取某个值时，函数与之对应的唯一确定的值。如当x=a时，函数有唯一确定的对应值，这个值就是当x=a时的函数值。

• 函数值的性质：
  ①当函数式是由一个解析式表示时，欲求函数值，实质就是求代数式的值；
  ②当一只函数解析式，又给出函数值，欲求相应的自变量的值时，实质就是解方程；
  ③当给定函数值的一个取值范围，欲求相应的自变量的取值范围时，实质就是解不等式；
  ④当自变量确定时，函数值时唯一确定的，但当函数值唯一确定时，对应的自变量可以是多个，如y=x²-1,当x=3时，x=±2。

考点名称：函数的图像

• 函数图象的概念：
  对于一个函数，如果把自变量x和函数y的每对对应值分别作为点的横坐标与纵坐标，在坐标平面内描出相应的点，这些点所组成的图形，就是这个函数的图象．

• 由函数解析式画其图象的一般步骤：
  ①列表：列表给出自变量与函数的一些对应值；
  ②描点：以表中每对对应值为坐标，在坐标平面内描出相应的点；
  ③连线：按照自变量由小到大的顺序，把所描各点用平滑的曲线连接起来．
  
  

  利用函数的图象解决实际问题，其关键是正确识别横轴和纵轴的意义，正确理解函数图象的性质，正确地识图、用图．
  
  函数图象上的点的坐标与其解析式之间的关系：
  ①由图象的定义可知图象上任意一点P（x，y）中的x，y是解析式方程的一个解，反之，以解析式方程的任意一个解为坐标的点一定在函数图象上；
  ②通常判定点是否在函数图象上的方法是：将这个点的坐标代入函数解析式，如果满足函数解析式，这个点就在函数的图象上，如果不满足函数解析式，这个点就不在其函数的图象上，反之亦然；
  ③两个函数图像的交点就是饿两个函数解析式所组成的方程组的解。

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。