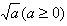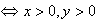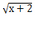一辆邮政车自A城驶往B城,沿途有n个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程-数学
题文
| 一辆邮政车自A城驶往B城,沿途有n个车站(包括起点A和终点B),该车在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该车站的邮包一个,还要装上该车站发给后面行程中每个车站的邮包一个.邮车在第1个车站 (A站)启程时要装上该站发给后面行程中每个车站的邮包(n-1)个,邮车上邮包总数是(n-1)个;邮车到第2个车站,卸下邮包1个,启程时要装上该站发给后面行程中每个车站的邮包(n-2)个,邮车上邮包总数是______(个). (1)邮车到第4个车站,启程时计算出邮车上邮包个数; (2)邮车到第x个车站,启程时邮车上邮包总数是多少(用x,n表示)? (3)当n=18,x=9时,求出邮车上邮包的个数. |
答案
| (1)在第1个车站(x=1)启程时邮包的总个数:n-1; 在第2个车站(x=2)启程时邮包的总个数:n-1-1+n-2=2(n-2); 在第3个车站(x=3)启程时邮包的总个数:2(n-2)-2+n-3=3(n-3); 在第4个车站(x=4)启程时邮包的总个数:3(n-3)-3+n-4=4(n-4); … 在第4个车站启程时邮包的总个数x(n-x); 故邮车到第4个车站,启程时计算出邮车上邮包个数为:4(n-4); (2)由(1)可得:邮车到第x个车站,启程时邮车上邮包总数是x(n-x)个. (3)当n=18,x=9时,x(n-x)=81, 故当n=18,x=9时,邮车上邮包的个数是81个. |
据专家权威分析,试题“一辆邮政车自A城驶往B城,沿途有n个车站(包括起点A和终点B),该车..”主要考查你对 函数值 等考点的理解。关于这些考点的“档案”如下:
函数值
考点名称:函数值
- 定义:
函数的值是指自变量在其取值范围内取某个值时,函数与之对应的唯一确定的值。如当x=a时,函数有唯一确定的对应值,这个值就是当x=a时的函数值。 - 函数值的性质:
①当函数式是由一个解析式表示时,欲求函数值,实质就是求代数式的值;
②当一只函数解析式,又给出函数值,欲求相应的自变量的值时,实质就是解方程;
③当给定函数值的一个取值范围,欲求相应的自变量的取值范围时,实质就是解不等式;
④当自变量确定时,函数值时唯一确定的,但当函数值唯一确定时,对应的自变量可以是多个,如y=x2-1,当x=3时,x=±2。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:所挂物体的质量/千克012345678弹簧的长度/cm1212.51313.51414.51515.516(1)弹簧不挂物体时的-数学
下一篇:我省是水资源比较缺乏的省份之一,为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段达到节约用水的目的,其中,某市规定如下用水收费标准:每户每月的用水量-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |