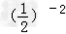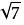濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
(1)计算:|-5|+3sin30°-(-6)2+(tan45°)-1(2)计算:在△ABC中,∠C=90°,求证:sinA+B2=cosC2.-数学
题文
(1)计算:|-5|+3sin30°-(-
(2)计算:在△ABC中,∠C=90°,求证:sin
|
答案
(1)原式=5+
(2)证明: 在△ABC中, ∵∠C=90°, ∴∠A+∠B=90°, ∴sin
∵cos
∴sin
|
据专家权威分析,试题“(1)计算:|-5|+3sin30°-(-6)2+(tan45°)-1(2)计算:在△ABC中,∠C=90..”主要考查你对 零指数幂(负指数幂和指数为1),特殊角三角函数值 等考点的理解。关于这些考点的“档案”如下:
零指数幂(负指数幂和指数为1)特殊角三角函数值
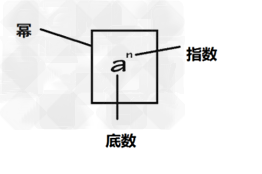
考点名称:零指数幂(负指数幂和指数为1)
- 零指数幂定义:任何不等于零的数的零次幂都等于1。
负指数幂的定义:任何不等于零的数的-n(n为正整数)次幂,等于这个数的n次幂的倒数。
指数为1:任何不等于零的数的1次幂,所得结果都等于这个数的本身。
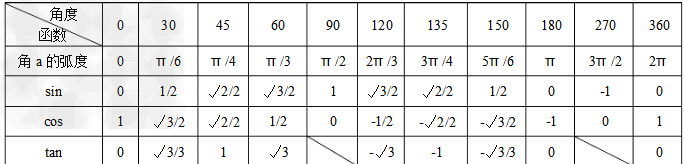
考点名称:特殊角三角函数值
- 特殊角三角函数值表:

- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |