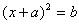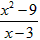题文
| 已知a、b、c是实数.若、、之和恰等于1,求证:这三个分数的值有两个为1,一个为-1. |
题型:解答题 难度:中档
答案
证明:由题设得:
++=1,
即(-1)+(-1)+(+1)=0,
∴++=0,
∴++=0,
∴| a(b-c+a)(b-c-a)+b(a-c+b)(a-c-b) | | 2abc |
+=0,
∴| (a+b-c)(ab-ac-a2+ab-bc-b2+ac+bc+c2) | | 2abc |
=0,
∴=0,
∴| (a+b-c)(c+a-b)(c-a+b) | | 2abc |
=0,
∴a+b-c=0或c-a+b=0或c+a-b=0,
(1)若a+b-c=0,则
==1,
==1,
==-1,
(2)若c+a-b=0,同理可得:
=1,=-1,=1,
(3)若b+c-a=0,同理可得:
=-1,=1,=1,
综上所述(1)、(2)、(3)可得,三个分数,
、、
的值有两个为1,一个为-1. |
据专家权威分析,试题“已知a、b、c是实数.若b2+c2-a22bc、c2+a2-b22ca、a2+b2-c22ab之和..”主要考查你对 分式的加减乘除混合运算及分式的化简 等考点的理解。关于这些考点的“档案”如下:
分式的加减乘除混合运算及分式的化简
考点名称:分式的加减乘除混合运算及分式的化简

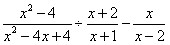
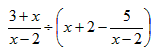
![化简:[+÷(+)2]×=()-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/87/2019-04-11/175852c8718f091c13116e9a9ba0bd6a.png)