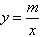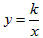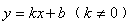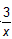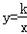题文

如图①，小华设计了一个探索杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A，在中点O的右侧用一个弹簧秤向下拉木杆，改变弹簧秤与点O的距离x（单位：厘米），观察弹簧秤的示数y（单位：牛）的变化情况，实验数据记录如下： x（单位：厘米） … 10 15 20 25 30 … y（单位：牛） … 30 20 15 12 10 … （1）把上表中（x，y）的各组对应值作为点的坐标，在图②所示的坐标系中描出相应的点，用平滑曲线连接这些点并观察所得的图象，猜测y与x之间的函数关系，并求出函数关系式； （2）当弹簧秤的示数为24牛时，弹簧秤与点O的距离是多少厘米？随着弹簧秤与O点的距离不断减小，弹簧秤的示数将发生怎样的变化？

题型：解答题  难度：中档

答案

（1）图象如右图： 由图象猜测y与x之间的函数关系为反比例函数 ∴设y= k x （k≠0） 把x=10，y=30代入得：k=300 ∴y= 300 x 将其余各点代入验证均适合 ∴y与x的函数关系式为：y= 300 x ． （2）把y=24代入y= 300 x 得：x=12.5 ∴当弹簧秤的示数为24N时，弹簧秤与O点的距离是12.5cm， 随着弹簧秤与O点的距离不断减小，弹簧秤上的示数不断增大．

据专家权威分析，试题“如图①，小华设计了一个探索杠杆平衡条件的实验：在一根匀质的木杆..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。