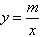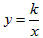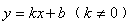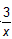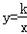题文

已知在直角坐标平面内有双曲线y= 6 3 x ，另有△ABC，其中点A、B、C的坐标分别是A（-2 2 ， 3 6 2 ），B（-2 2 ，0），C（0， 3 6 2 ）． （1）如果将△ABC沿x轴翻折后得到对应的△A1B1C1 （其中点A、B、C的对应点分别是点A1、B1、C1），问：△A1B1C1的三个顶点中，有无在双曲线y= 6 3 x 上的点？若有，写出这个点的坐标． （2）如果将△ABC沿x轴正方向平移a个单位后，使△ABC的一个顶点落在双曲线y= 6 3 x 上，请直接写出a的值． （3）如果△ABC关于原点O的对称的三角形△A2B2C2（其中点A、B、C的对应点分别是点A2、B2、C2），请写出经过点A、A2的直线所表示的函数解析式．

题型：解答题  难度：中档

答案

（1）根据关于x轴对称的点的坐标特点，可得A1的坐标为（-2 2 ，- 3 6 2 ），B1的坐标为（-2 2 ，0），A1的坐标为（0，- 3 6 2 ）， 将三点代入双曲线y= 6 3 x ，只有点A1，符合解析式，此时左边=- 3 6 2 ，右边= 6 3 -2 2 =- 3 6 2 ，左边=右边． 故有在双曲线上的点，这个点是A1，它的坐标为（-2 2 ，- 3 6 2 ）； （2）①平移后点A的对应点在双曲线上，此时点A的对应点的坐标为（-2 2 +a， 3 6 2 ）， 代入解析式得： 3 6 2 = 6 3 -2 2 +a ， 解得：a=4 2 ； ②平移后点C的对应点在双曲线上，此时点A的对应点的坐标为（a， 3 6 2 ）， 代入解析式得： 3 6 2 = 6 3 a ， 解得：a=2 2 ； 综上可得a=2 2 或a=4 2 ； （3）点A（-2 2 ， 3 6 2 ）关于原点对称的点A2的坐标为（2 2 ，- 3 6 2 ）， 设过点A、A2的直线解析式为y=kx+b，则 -2 2 k+b= 3 6 2 2 2 k+b=- 3 6 2 ， 解得： a=- 3 3 4 b=0 ， 故直线AA2的解析式是y=- 3 3 4 x．

据专家权威分析，试题“已知在直角坐标平面内有双曲线y=63x，另有△ABC，其中点A、B、C的..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。