对下列说法谈谈你的看法:(1)某彩票的中奖机会是2%,如果我买10000张彩票一定有200张会中奖;(2)我和同学玩飞行棋游戏,我掷了20次骰子还没掷得“6点”,说明我掷得“6点”的机会-数学
题文
| 对下列说法谈谈你的看法: (1)某彩票的中奖机会是2%,如果我买10000张彩票一定有200张会中奖; (2)我和同学玩飞行棋游戏,我掷了20次骰子还没掷得“6点”,说明我掷得“6点”的机会比其他同学掷得“6点”的机会小; (3)我们知道,抛掷一枚普通硬币得到正面和反面的机会各为50%,出就是说,虽然没人能保证抛掷1000次会得到500次正面和500次反面,但是,我敢保证得到正面的次数会非常接近得到反面的次数. |

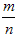 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。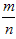 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1;