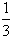将分别标有1、2、3、4、5的五个同样大小的球放人袋子中,由甲、乙各摸一个球(第一个摸后不放回),计算两球数字之和,若和为偶数,则甲胜,否则乙胜。(1)你认为这个游戏规则对-九年级数学
题文
| 将分别标有1、2、3、4、5的五个同样大小的球放人袋子中,由甲、乙各摸一个球(第一个摸后不放回),计算两球数字之和,若和为偶数,则甲胜,否则乙胜。 (1)你认为这个游戏规则对双方来说公平吗?若不公平,谁获胜的机会大; (2)甲、乙谁先摸,会影响结果吗? (3)若不公平,你能利用这五个球设计一个较为合理的公平的游戏吗?试一试。 |
答案
| 解:(1)不公平,乙获胜的机会较大 因为和为偶数,两次摸出球上的数字必须是(1,3),(1,5),(2,4),(3,5)共四种可能, 但和为奇数,一共有(1,2),(1,4),(2,3),(2,4), (3,4),(4,5)共六种可能 因此P(和为偶数)=  ,P(和为奇数)= ,P(和为奇数)= ; ;(2)不会影响,因为两数之和不会随次序改变的; (3)游戏规则:将分别标有1、2、3、4、5的五个同样大小的球放人袋中,由甲、乙各摸一次,同时取出两个球。(摸出后放回) 数字之和为5,则甲胜,数字之和为7,则乙胜。(答案不唯一) |
据专家权威分析,试题“将分别标有1、2、3、4、5的五个同样大小的球放人袋子中,由甲、乙..”主要考查你对 利用概率解决问题 等考点的理解。关于这些考点的“档案”如下:
利用概率解决问题
考点名称:利用概率解决问题
- 应用概率可以解决以下问题:
(1)彩票中奖率的问题;
(2)抽样检测中产品合格率的问题;
(3)天气预报降水的概率;
(4)抛硬币、掷骰字的问题;
(5)圆盘分几个区域,分别涂色,转到哪个颜色的区域的概率;
(6)有刚回及无放回的摸球问题。
概率的应用情况远不止于这些,还有很多类似情况,在解决这类问题时,要充分理解题意,找到切入点,就能轻松的解决问题。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:从一个图书仓库里随意抽取100本书,按内容可为文科、理科2类,按装潢分为精装、平装2种,其中文科40本,精装书70本,理科的平装书20本。(1)求任取1本恰是文科精装的概率;(2-九年级数学
下一篇:口袋里有15个球,其中白球有x个,绿球有2x个,其余为黑球,甲从袋中任意摸出1个球,若为绿球则获胜;甲将摸出的球放回袋中,乙从袋中摸出1个球,若为黑球则获胜。(1)当x为何-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![如图,转动转盘,转盘停止转动时指针指向阴影部分的概率是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/571e82d5a6a0366b53423682fba5f64b.gif)
![一个均匀的立方体六个面上分别标有数1,2,3,4,5,6。下图是这个立方体表面的展开图。抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的的概率是[]A、B、C、D、-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/afe03013805201dd7c0a3b8b6d39e531.gif)
![从编号为1到10的10张卡片中任取1张,所得编号是3的倍数的概率为[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-20/1bb75c757d66c522ea7ffc15841e3462.gif)
![在一个暗箱里,装有3个红球、5个黄球和7个绿球,它们除颜色外都相同,搅拌均匀后,从中任意摸出一个球是红球的概率是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/116/2019-05-19/f0e84e9d734a37a2633ed58d0df722b9.gif)