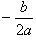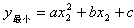如(图1),在平面直角坐标系中,已知点,点在x正半轴上,且.动点在线段上从点向B点以每秒个单位的速度运动,点M、N在x轴(M在点N的左侧),以P、M、N为顶点的三角形是等边三角形-九年级数学
题文
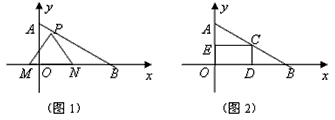
如(图1),在平面直角坐标系中,已知点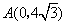 ,点 ,点 在x正半轴上,且 在x正半轴上,且 .动点 .动点 在线段 在线段 上从 上从 点向B点以每秒 点向B点以每秒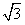 个单位的速度运动,点M、N在x轴(M在点N的左侧),以P、M、N为顶点的三角形是等边三角形,设运动时间为秒. 个单位的速度运动,点M、N在x轴(M在点N的左侧),以P、M、N为顶点的三角形是等边三角形,设运动时间为秒. (1) 求直线 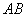 的解析式; 的解析式; (2)求等边  的边长(用 的边长(用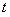 的代数式表示),并求出当等边 的代数式表示),并求出当等边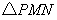 的顶点 的顶点 运动到与原点 运动到与原点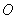 重合时 重合时 的值; 的值; (3)如果取 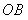 的中点 的中点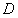 ,以 ,以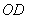 为边在 为边在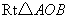 内部作如图2所示的矩形 内部作如图2所示的矩形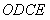 ,点 ,点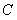 在线段 在线段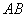 上.设等边 上.设等边 和矩形 和矩形 重叠部分的面积为 重叠部分的面积为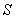 ,请求出当 ,请求出当 秒时 秒时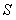 与 与 的函数关系式,并求出 的函数关系式,并求出 的最大值. 的最大值. |
|
|
答案
解:(1)直线的解析式为: . .(2)  , ,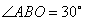 , ,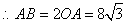 , ,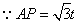 , ,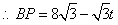 , ,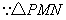 是等边三角形, 是等边三角形, , ,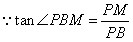 , ,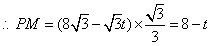 . .当点 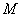 与点N重合时, 与点N重合时,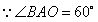 , ,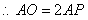 . .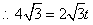 , ,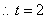 . .(3)①当  时,见图2. 时,见图2.设 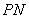 交 交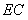 于点H,重叠部分为直角梯形 于点H,重叠部分为直角梯形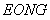 , ,作
上一篇:二次函数的最小值是().-九年级数学
下一篇:研究表明一种培育后能繁殖的细胞在一定的环境下有以下规律:若有n个细胞,经过第一周期后,在第1个周期内要死去1个,会新繁殖(n-1)个;经过第二周期后,在第2个周期内要死去2-九年级数学
零零教育社区:论坛热帖子
|

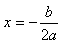
![已知(m为任意实数),则P、Q的大小关系为[]A.P>QB.P=QC.P<QD.不能确定-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/119/2019-12-17/a2d88dc8111889192d90ae38a9b84704.gif)