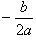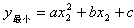已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,-)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0。(1)求c的值;(2)设抛物线y=ax2+bx+c与x轴-九年级数学
题文
|
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,- |
|
|
| (1)求c的值; (2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值; (3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(x0,y0),求这时|y0|的最小值。 |
答案
|
解:(1)∵(0,- |

 )和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0。
)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0。
 )在y=ax2+bx+c上,
)在y=ax2+bx+c上, =a×02+b×0+c,
=a×02+b×0+c, ;
;
 =a(m-b)2+b(m-b)-
=a(m-b)2+b(m-b)- ,
, )重合,与题意不合
)重合,与题意不合 ,
, )>0,
)>0, ;
; 的对称轴为x=
的对称轴为x= ,最小值为
,最小值为 ,
, 在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h,
在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h, <-1,即b>2时,在x轴上方与x轴距离最大的点是(1,y0),
<-1,即b>2时,在x轴上方与x轴距离最大的点是(1,y0), +b>
+b> ,
, >
> ,
, ;
; ≤0,即0≤b≤2时,
≤0,即0≤b≤2时, +b≥
+b≥ ,当b=0时等号成立,
,当b=0时等号成立, ),
), |=
|= ≥
≥ ,当b=0时等号成立,
,当b=0时等号成立, ≤1,即-2≤b<0时,
≤1,即-2≤b<0时, |=|
|=| -b>
-b> ),
),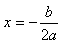
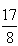
![已知(m为任意实数),则P、Q的大小关系为[]A.P>QB.P=QC.P<QD.不能确定-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/119/2019-12-17/a2d88dc8111889192d90ae38a9b84704.gif)