题文

如图，两块三角板摆放在一起，射线OM平分∠BOC、ON平分∠AOC． （1）求∠MON的度数； （2）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOC=20°，其它条件不变，求∠MON的度数； （3）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOC=α，（α为锐角），其它条件不变，求∠MON的度数； （4）如果（1）中，一个三角板绕点O旋转一定角度，使得∠AOB=β（β为锐角），其它条件不变，求∠MON的度数．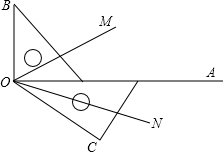

题型：解答题  难度：中档

答案

（1）∵∠BOC=∠AOB+∠AOC=90°+30°=120°，射线OM平分∠BOC， ∴∠COM= 1 2 ∠BOC= 1 2 ×120°=60°， ∵ON平分∠AOC， ∴∠CON= 1 2 ∠AOC= 1 2 ×30°=15°， ∴∠MON=∠COM-∠CON=60°-15°=45°； （2）∵∠BOC=∠AOB+∠AOC=90°+20°=110°，射线OM平分∠BOC， ∴∠COM= 1 2 ∠BOC= 1 2 ×110°=55°， ∵ON平分∠AOC， ∴∠CON= 1 2 ∠AOC= 1 2 ×20°=10°， ∴∠MON=∠COM-∠CON=55°-10°=45°； （3）∵∠BOC=∠AOB+∠AOC=90°+α，射线OM平分∠BOC， ∴∠COM= 1 2 ∠BOC= 1 2 ×（90°+α）， ∵ON平分∠AOC， ∴∠CON= 1 2 ∠AOC= 1 2 α， ∴∠MON=∠COM-∠CON= 1 2 ×（90°+α）- 1 2 α=45°+ 1 2 α- 1 2 α=45°； （4））∵∠BOC=∠AOB+∠AOC=β+30°，射线OM平分∠BOC， ∴∠COM= 1 2 ∠BOC= 1 2 （β+30°）， ∵ON平分∠AOC， ∴∠CON=  1/2    1 2 下一页 尾页 初中数学考试题 解答题 平分 射线 度数 最新内容 相关内容 网友推荐 图文推荐 填空，完成下列说理过程如图，DP平(2019-12-31) 如图，已知直线AB，OA平分∠COD，O(2019-12-31) 如图所示，OE，OD分别平分∠AOC和∠(2019-12-31) 如图，O是直线AB上的一点，OD是∠A(2019-12-31) 如图，∠AOB=110°，∠COD=70°，O(2019-12-31) 请完成下面的说明：（1）如图①所示(2019-12-31) 如图所示，两块三角板的直角顶点O重(2019-12-31) 如图，AO⊥BC，DO⊥OE，OF平分∠AO(2019-12-31) 如图所示，OE，OD分别平分∠AOB和∠(2019-12-31) 如图，某同学在课桌上随意将一块三角板的直角叠放在直 如图，已知，∠AOE=∠COD，且射线OC平分∠AOE的补角∠ 如图，∠AOB=90°，∠BOC=42°，OD平分∠AOC．求∠AOD 如图所示，∠AOB=70°，∠COD=80°，求∠AOD-∠BOC的度 如图，OC平分∠BOD，OE平分∠AOD，则与∠COD互余的角是 如图，∠AOB=42゜，∠BOC=86゜，OD为∠AOC的平分线，求 如图，∠AOB=90°，OD平分∠BOC，∠AOC=2∠1，则∠1=（ 如图，O为直线AB上一点，∠AOC=48°，OD平分∠AOC，∠ 如图所示，O是直线AC上一点，OB是一条射线，OD平分∠A 如图，O是直线AB上一点，OC为任意一条射线，∠BOC=40° 如图，OA⊥OB，∠BOC=40°，OD平分(2019-12-31) 下列情形的角平分线，互相垂直的是(2019-12-31) 如图，直线AB、CD相交于点O，OF平分(2019-12-31) 如图，将长方形纸片ABCD沿EF，DE对(2019-12-31) 已知∠AOC=2∠BOC，若∠BOC=30°，(2019-12-31) 如图所示，BE是∠MBC的平分线，CE是(2019-12-31) 如图所示，已知∠AOC=∠COD=∠BOD，(2019-12-31) 如图，已知CD⊥AB于点D，BE⊥AC于点(2019-12-31) 如图，AD⊥BC于点D，EG⊥BC于点G，(2019-12-31) 已知α=76°5′，β=76.5°，则α与(2019-12-31) 1 2 下列情形的角平分线，互相垂 如图，直线AB、CD相交于点O， 如图，将长方形纸片ABCD沿EF 如图所示，BE是∠MBC的平分线 如图所示，已知∠AOC=∠COD= 上一篇：如图，O是直线AB上一点，OC为任意一条射线，∠BOC=40°，OE平分∠AOC，OD平分∠BOC，则∠DOE的度数为（）A．70゜B．80゜C．90゜D．100゜-数学     下一篇：如图，O是直线AB上一点，若∠BOC=51°38′，则∠AOC=______．-数学 零零教育社区：论坛热帖子 [家长教育] 孩子为什么会和父母感情疏离？ (2019-07-14) [教师分享] 给远方姐姐的一封信 (2018-11-07) [教师分享] 伸缩门 (2018-11-07) [教师分享] 回家乡 (2018-11-07) [教师分享] 是风味也是人间 (2018-11-07) [教师分享] 一句格言的启示 (2018-11-07) [教师分享] 无规矩不成方圆 (2018-11-07) [教师分享] 第十届全国教育名家论坛有感（二） (2018-11-07) [教师分享] 贪玩的小狗 (2018-11-07) [教师分享] 未命名文章 (2018-11-07) 栏目导航 有理数定义及分类 正数与负数 数轴 相反数 绝对值 比较有理数的大小 倒数 有理数加法 有理数减法 有理数的加减混合运算 有理数乘法 有理数除法 有理数的乘除混合运算 有理数的乘方 有理数的混合运算 近似数和有效数字 科学记数法和有效数字 实数的比较大小 无理数的定义 估算无理数的大小 实数的定义 数学常识 计算器的使用 写代数式 代数式的求值 去括号与添括号 整式的加减 单项式 多项式 同类项 探索规律 代数式的概念 整式的定义 一元一次方程的定义 一元一次方程的解法 一元一次方程中的待定系数 一元一次方程的应用 等式的性质 方程的定义 方程的解 等式的定义 二元一次方程的定义 二元一次方程组的定义 二元一次方程组的解法 二元一次方程组的应用 二元一次方程的应用 二元一次方程的解法 不等式的定义 不等式的性质 一元一次不等式的解法 一元一次不等式组的定义 一元一次不等式组的解法 一元一次不等式组的应用 不等式待定系数的取值范围 不等式的比较大小 一元一次不等式的应用 一元一次不等式的定义 函数的定义 变量及函数 常量与变量 函数值 函数的图像 正比例函数的定义 正比例函数的图像 一次函数的定义 一次函数的图像 求一次函数的解析式及一次函数的应用 一次函数与一元一次不等式（一元一次方程） 合并同类项 零指数幂（负指数幂和指数为1） 整式的乘法 整式的除法 公因式 因式分解 平方差公式 完全平方公式 整式的加减乘除混合运算 分式的定义 最简公分母 最简分式 分式的基本性质 分式的乘除 分式的加减 分式方程的定义 解分式方程 分式方程的应用 分式的加减乘除混合运算及分式的化简 反比例函数的定义 反比例函数的图像 反比例函数的性质 求反比例函数的解析式及反比例函数的应用 平均数 中位数和众数 极差 方差 二次根式的定义 二次根式的乘除 二次根式的加减 平方根 立方根 算术平方根 同类二次根式 二次根式的加减乘除混合运算，二次根式的化简 最简二次根式 实数的运算 一元二次方程的定义 一元二次方程的解法 一元二次方程根与系数的关系 一元二次方程的应用 一元二次方程根的判别式 随机事件 必然事件 概率的意义 列举法求概率 利用频率估算概率 利用概率解决问题 二次函数的定义 二次函数的图像 二次函数的最大值和最小值 求二次函数的解析式及二次函数的应用 二次函数与一元二次方程 二次函数与不等式（组） 全面调查和抽样调查 频数与频率 直方图 条形图 扇形图 折线图 统计表 象形统计图 总体、个体、样本、样本容量 用样本估算总体 二元多次（二次以上）方程（组） 逻辑推理 三元（及三元以上）一次方程（组）的解法 三元（及三元以上）一次方程（组）的应用 直线，线段，射线 角的概念 角平分线的定义 余角，补角 看图形找规律 认识立体几何图形 认识平面图形 几何体的展开图 几何体的表面积，体积 点、线、面、体 截一个几何体 七巧板 对顶角，同位角，内错角，同旁内角 平行线的判定 平行线的性质，平行线的公理 平行线之间的距离 垂直的判定与性质 相交线 三角形的内角和定理 三角形的外角性质 三角形的稳定性 三角形的中线，角平分线，高线，垂直平分线 三角形的内心、外心、中心、重心 直角三角形的性质及判定 等腰三角形的性质，等腰三角形的判定 等边三角形 三角形的周长和面积 三角形的三边关系 三角形中位线定理 全等三角形的性质 三角形全等的判定 全等图形 用坐标表示轴对称 轴对称 勾股定理的逆定理 勾股定理 平行四边形的性质 平行四边形的判定 矩形，矩形的性质，矩形的判定 菱形，菱形的性质，菱形的判定 梯形，梯形的中位线 重心 正方形，正方形的性质，正方形的判定 中心对称 关于原点对称的点的坐标 图形旋转 垂直于直径的弦 圆心角，圆周角，弧和弦 点与圆的位置关系 直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离） 圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切） 正多边形和圆（内角，外角，中心角，边心距，边长，周长，面积的计算） 弧长的计算 扇形面积的计算 圆锥的计算 圆柱的计算 圆的认识 确定圆的条件 相似多边形的性质 相似三角形的判定 相似三角形的性质 相似三角形的应用 位似 黄金分割数 相似图形 比例的性质 平行线分线段成比例 解直角三角形 锐角三角函数的定义 特殊角三角函数值 同角三角函数的关系 互余两角三角函数的关系 投影 视图（盲区） 尺规作图 有序数对 用坐标表示位置 用坐标表示平移 平面直角坐标系 平面向量 多边形的内角和和外角和 平面图形的平铺和镶嵌 组合图形面积 多边形 命题，定理 平移 角平分线的性质 垂直平分线的性质 最新信息 填空，完成下列说理过程如图，DP平 如图，已知直线AB，OA平分∠COD，O 如图所示，OE，OD分别平分∠AOC和∠ 如图，O是直线AB上的一点，OD是∠A 如图，∠AOB=110°，∠COD=70°，O 请完成下面的说明：（1）如图①所示 如图所示，两块三角板的直角顶点O重 如图，AO⊥BC，DO⊥OE，OF平分∠AO 如图所示，OE，OD分别平分∠AOB和∠ （1）如图a，①已知AB∥CD，∠ABC= 热门信息 如图，OA⊥OB，∠BOC=40°，OD平分 下列情形的角平分线，互相垂直的是 如图，直线AB、CD相交于点O，OF平分 如图，将长方形纸片ABCD沿EF，DE对 已知∠AOC=2∠BOC，若∠BOC=30°， 如图所示，BE是∠MBC的平分线，CE是 如图所示，已知∠AOC=∠COD=∠BOD， 如图，已知CD⊥AB于点D，BE⊥AC于点 如图，AD⊥BC于点D，EG⊥BC于点G， 已知α=76°5′，β=76.5°，则α与 Copyright 2021 零零教育信息网 @ Powered By 零零教育信息网 ，这是一个公共的免费分享平台 网站导航联系我们广告合作豫ICP备09039788号 个人中心 服务邮箱 服务邮箱 7720015@qq.com 微信咨询 返回顶部 网站首页 联系我 微信咨询 个人中心 X 截屏，微信识别二维码 微信号：ten00_cn （点击微信号复制，添加好友）   打开微信 微信号已复制，请打开微信添加咨询详情！ 新闻 图书