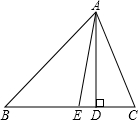
如图,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有_________个,它们分别是_________.∠A=_________,根据是_________-七年级数学
题文
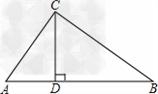
| 如图,∠ACB=90 °,CD⊥AB,则图中与∠A互余的角有 _________ 个,它们分别是 _________ .∠A= _________ ,根据是 _________ |
 |
答案
| 两 ; ∠ACD和∠B ;∠BCD ; 同角的余角相等 . |
据专家权威分析,试题“如图,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有_________个,它们..”主要考查你对 三角形的内角和定理,余角,补角 等考点的理解。关于这些考点的“档案”如下:
三角形的内角和定理余角,补角
考点名称:三角形的内角和定理
- 三角形的内角和定理及推论:
三角形的内角和定理:三角形三个内角和等于180°。
推论:
(1)直角三角形的两个锐角互余。
(2)三角形的一个外角等于和它不相邻的来两个内角的和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
注:在同一个三角形中:等角对等边;等边对等角;大角对大边;大边对大角。
考点名称:余角,补角
余角:
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A
补角:
如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角
∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A- 补角的性质:
同角的补角相等。比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:
同角的余角相等。比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:
①钝角没有余角;
②互为余角、补角是两个角之间的关系。如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;
③互为余角、补角只与角的度数相关,与角的位置无关。只要它们的度数之和等于90°或180°,就一定互为余角或补角。 - 余角与补角概念认识提示:
(1)定义中的“互为”一词如何理解?
如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 , 同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图,五角星的顶点分别是A,B,C,D,E,那么∠A+∠B+∠C+∠D+∠E=()-七年级数学
下一篇:如图所示,在△ABC中,∠C=∠1,∠A=∠2(1)求∠DBC的度数;(2)试说明BD平分∠ABC-七年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |