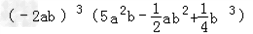题文
给定整数n≥3,实数a1,a2,…,an满足min1≤i<j≤n|ai-aj|=1.求| n |  | | k=1 |
|ak|3的最小值. |
题型:解答题 难度:中档
答案
不妨设a1<a2<…<an,则对1≤k≤n,有|ak|+|an-k+1|≥|an-k+1-ak|≥|n+1-2k|,
所以| n |  | | k=1 |
|ak|3=| n |  | | k=1 |
(|ak|3+|an+1-k|3)=| n |  | | k=1 |
(|ak|+|an+1-k|)((|ak|-|an+1-k|)2+(|ak|+|an+1-k|)2)≥| n |  | | k=1 |
(|ak|+|an+1-k|)3≥| n |  | | k=1 |
|n+1-2k|3.
当n为奇数时,| n |  | | k=1 |
|n+1-2k|3=2?23? |  | | i=1 |
i3=(n2-1)2.
当n为偶数时,| n |  | | k=1 |
|n+1-2k|3=2 |  | | i=1 |
(2i-1)3=2(| n |  | | j=1 |
j3- |  | | i=1 |
(2i)3)=n2(n2-2).
所以,当n为奇数时,| n |  | | k=1 |
|ak|3≥(n2-1)2,当n为偶数时,| n |  | | k=1 |
|ak|3≥n2(n2-2),等号均在ai=i-,i=1,2,n时成立.
因此,| n |  | | k=1 |
|ak|3的最小值为(n2-1)2(n为奇数),或者n2(n2-2)(n为偶数). |
据专家权威分析,试题“给定整数n≥3,实数a1,a2,…,an满足min1≤i<j≤n|ai-aj|=1.求nk=1..”主要考查你对 整式的加减乘除混合运算 等考点的理解。关于这些考点的“档案”如下:
整式的加减乘除混合运算
考点名称:整式的加减乘除混合运算



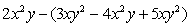
![化简-(-2a+4b-c)的结果为[]A.2a+4b-cB.2a-4b-cC.2a-4b+cD.-2a+4b-c-七年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/77/2019-04-06/f85462bbc3efb07bd59e9b75839bd034.png)