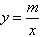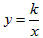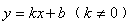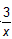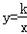题文

如图，矩形ABCD中，AB=5，AD=3，E是CD上一点（不与C，D重合），连接AE，过点B作BF⊥AE， 垂足为F． （1）若DE=2，求 BF AB 的值； （2）设AE=x，BF=y． ①求y关于x的函数解析式，写出自变量x的取值范围； ②问当点E从D运动到C，BF的值是增大还是减小？说明理由． ③当△AEB为等腰三角形时，求BF的长．

题型：解答题  难度：中档

答案

（1）∵DE=2，AD=3， ∴AE= 13 ， ∵△ABF∽△EDA ∴ BF AB = AD AE = 3 13 13 ； （2）根据（1）可知： ① 5 x = y 3 即y= 15 x ，3＜x＜ 34 ； ②减小，因为y= 15 x 中，y随x的增大而减小； ③当△AEB为等腰三角形时，有3种情况： a、当AB=BE时，则BE=5，则CE=4，DE=1，AE= 10 ，AF= 10 2 ，∴BF= 3 10 2 ； b、当AE=BE时，E为CD中点，则DE=2.5，AE= 61 2 ，所以BF= 30 61 61 ； c、当AB=AE=5时，△ABF≌△AED，则BF=AD=3． 所以BF的值为： 3 10 2 或 30 61 61 或3．

据专家权威分析，试题“如图，矩形ABCD中，AB=5，AD=3，E是CD上一点（不与C，D重合），连接..”主要考查你对  求反比例函数的解析式及反比例函数的应用，矩形，矩形的性质，矩形的判定  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用矩形，矩形的性质，矩形的判定

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。

考点名称：矩形，矩形的性质，矩形的判定

• 矩形:
  是一种平面图形，矩形的四个角都是直角，同时矩形的对角线相等，而且矩形所在平面内任一点到其两对角线端点的距离的平方和相等。

• 矩形的性质：
  1．矩形的4个内角都是直角；
  2．矩形的对角线相等且互相平分；
  3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等；
  4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线），它至少有两条对称轴。对称中心是对角线的交点。
  5．矩形是特殊的平行四边形，矩形具有平行四边形的所有性质
  6.顺次连接矩形各边中点得到的四边形是菱形

• 矩形的判定：
  ①定义：有一个角是直角的平行四边形是矩形
  ②定理1：有三个角是直角的四边形是矩形
  ③定理2：对角线相等的平行四边形是矩形
  ④对角线互相平分且相等的四边形是矩形
  矩形的面积：S_矩形=长×宽=ab。

• 黄金矩形:
  宽与长的比是（√5-1）/2（约为0.618）的矩形叫做黄金矩形。
  黄金矩形给我们一协调、匀称的美感。世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计。如希腊的巴特农神庙等。