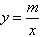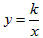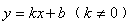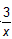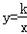题文

等边△OAB和△AEF的一边都在x轴上，双曲线y= k x （k＞0）经过边OB的中点C和AE的中点D．已知：OA=2，则△AEF的边长为______．

题型：填空题  难度：中档

答案

过C作CG⊥x轴，过D作DH⊥x轴， ∵△OAB为等边三角形，OA=2，C为OB的中点， ∴∠BOA=60°，OC=1， 在Rt△OCG中，sin∠BOA= CG OC ，cos∠BOA= OG OC ， ∴CG=OC?sin∠BOA= 3 2 ，OG=OC?cos∠BOA= 1 2 ， ∴C（ 1 2 ， 3 2 ）， 将C坐标代入反比例解析式中得：k= 3 4 ， ∴反比例解析式为y= 3 4x ， 设等边△AEF的边长为a， ∵△AEF为等边三角形，AE=AF=EF=a，C为OB的中点， ∴∠EAF=60°，AD= 1 2 a， 同理得到AH= 1 4 a，DH= 3 4 a， ∴OH=OA+AH=2+ 1 4 a， ∴D（2+ 1 4 a， 3 4 a）， 代入反比例函数解析式得： 3 4 a（2+ 1 4 a）= 3 4 ，即a（2+ 1 4 a）=1， 整理得：8a+a2=4，即a2+8a-4=0， 解得：a= -8±4 5 2 =-4±2 5 ， 而a=-4-2 5 不合题意，舍去，故a=-4+2 5 ， 则等边△AEF的边长为-4+2 5 ． 故答案为：-4+2 5 ．

据专家权威分析，试题“等边△OAB和△AEF的一边都在x轴上，双曲线y=kx（k＞0）经过边OB的中点..”主要考查你对  求反比例函数的解析式及反比例函数的应用  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用

考点名称：求反比例函数的解析式及反比例函数的应用

• 反比例函数解析式的确定方法：
  由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

  反比例函数的应用：
  建立函数模型，解决实际问题。

• 用待定系数法求反比例函数关系式的一般步骤是：
  ①设所求的反比例函数为：y= (k≠0)；
  ②根据已知条件（自变量与函数的对应值）列出含k的方程；
  ③由代人法解待定系数k的值；
  ④把k值代人函数关系式y= 中。
  
  反比例函数应用一般步骤：
  ①审题；
  ②求出反比例函数的关系式；
  ③求出问题的答案，作答。