题文

一枚硬币抛起后落地时，“正面朝上”的机会有多大？ （1）写出你的猜测； （2）一位同学在做这个实验时说：“我只做了10次实验，就得到了正面朝上的概率约为30%．”你认为他说的对吗？为什么？ （3）还有一位同学在做这个实验中觉得用硬币麻烦，改用可乐瓶盖做这个实验，你认为他的做法科学吗？为什么？

题型：解答题  难度：中档

答案

（1）正面向上的概率为 1 2 ； （2）不对， 因为试验次数较小，事件出现的频率与事件出现的机会有比较大的差距，不能据此估计事件发生的机会； （3）不科学， 因为实验的条件不同，硬币质地均匀，出现正面与反面的机会是均等的，而可乐瓶盖质地不均匀，实验条件不一样．

据专家权威分析，试题“一枚硬币抛起后落地时，“正面朝上”的机会有多大？（1）写出你的猜测..”主要考查你对  利用频率估算概率，二次函数的最大值和最小值  等考点的理解。关于这些考点的“档案”如下：

利用频率估算概率二次函数的最大值和最小值

考点名称：利用频率估算概率

• 在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率。
  注：
  （1）当试验的可能结果不是有限个，或各种结果发生的可能性不相等时，一般用统计频率的方法来估计概率；
  （2）利用频率估计概率的数学依据是大数定律：当试验次数很大时，随机事件A出现的频率，稳定地在某个数值P附近摆动.这个稳定值P，叫做随机事件A的概率，并记为P(A)=P。
  （3）利用频率估计出的概率是近似值。

考点名称：二次函数的最大值和最小值

• 二次函数的最值：
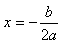  1.如果自变量的取值范围是全体实数，则当a>0时，抛物线开口向上，有最低点，那么函数在处取得最小值y_最小值=；
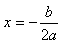  当a<0时，抛物线开口向下，有最高点，即当时，函数取得最大值，y_最大值=。
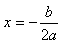  也即是：如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，。
  2.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当x=x₂ 时，，当x=x₁ 时；如果在此范围内，y随x的增大而减小，则当x=x₁时，，当x=x₂时 。