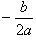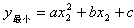已知直线与y轴交于点C,与x轴交于点A,(1)求线段AC的长度;(2)若抛物线过点C、A,且与x轴交于另一点B,将直线AC沿y轴向下平移m个单位长度,若平移后的直线与x轴交于点D,与抛-九年级数学
题文
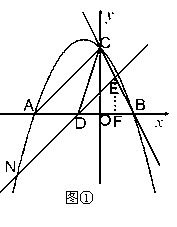
已知直线 与y轴交于点C,与x轴交于点A, 与y轴交于点C,与x轴交于点A,(1)求线段AC的长度; (2)若抛物线  过点C、A,且与x轴交于另一点B,将直线AC沿y轴向下平移m个单位长度,若平移后的直线与x轴交于点D,与抛物线交于点N(N在抛物线对称轴的左边),与直线BC交于点E. 过点C、A,且与x轴交于另一点B,将直线AC沿y轴向下平移m个单位长度,若平移后的直线与x轴交于点D,与抛物线交于点N(N在抛物线对称轴的左边),与直线BC交于点E.① 是否存在这样的m,使得△CAD是以AC为底的等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由; ② 在直线AC平移的过程中,是否存在m值,使得△CDE的面积最大, 若存在,请求出m值,若不存在,请说明理由。 |
|
|
答案
解:(1)当 时,y=4, ∴C(0,4) 时,y=4, ∴C(0,4)当y=0时,  ,∴A(-4,0) ,∴A(-4,0)在Rt△AOC中,OA=OC=4,∠AOC=90°, ∴AC=  ; ;(2)①抛物线经过点A、C, 则  解得 解得 ∴抛物线所对应的函数关系式为  ; ;∵△CAD是以AC为底的等腰三角形, ∴点D在AC的垂直平分线上,此时点D与原点重合,即D(0,0) ∴ 则平移后的直线所对应的函数关系式为y=x ∵点N是抛物线  与直线y=x的交点 与直线y=x的交点∴设点N(a,a), 则  ,解得 ,解得  ∵点N在抛物线对称轴的左侧, ∴N  ② 设△CDE的面积为S 在  中,令y=0, 中,令y=0,解得x= -4或x=2, ∴B(2,0), AB=6 当点D在点B的左侧时,即当  时(如图①) 时(如图①)平移后的直线为  ; ;当y=0时,x=m-4 ∴  ∴BD=2-(m-4)=6-m; ∴BD=2-(m-4)=6-m;过点E作EF⊥AB于点F,由DE∥AC,得∠BDE =∠CAD ∴ △BDE∽△BAC ∴  ∴ ∴  ; 解得 ; 解得 ; ;∴   ∴抛物线的开口向下,对称轴为直线m=3, ∵顶点(3,3)的横坐标在范围  内 内∴当  ,S有最大值为3; ,S有最大值为3;当点D在点B的右侧时,即当  时(如图②) 时(如图②)平移后的直线所对应的函数关系式为  , ,当y=0时,x=  ∴D(  ,0) ,0) ∴BD= 过点E作EG⊥AB于点G 由DE∥AC,得∠BDE =∠CAD ∴△BDE∽△BAC ∴  ,解得 ,解得 ∴   ∴抛物线开口向上,对称轴为m=3 ∵在抛物线对称轴的右侧,S随着的增大而增大。 ∴当  时, S没有最大值 时, S没有最大值综上得,在直线AC平移的过程中,不存在m值,使得△CDE的面积最大。 |
|
据专家权威分析,试题“已知直线与y轴交于点C,与x轴交于点A,(1)求线段AC的长度;(2)若..”主要考查你对 二次函数的最大值和最小值,求一次函数的解析式及一次函数的应用,求二次函数的解析式及二次函数的应用,平移 等考点的理解。关于这些考点的“档案”如下:
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件,市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件,设每件涨价元(为非负-九年级数学
下一篇:为了扶持大学生自主创业,某市政府提供了50万元无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款。已知该产品-九年级数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |



![已知(m为任意实数),则P、Q的大小关系为[]A.P>QB.P=QC.P<QD.不能确定-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/119/2019-12-17/a2d88dc8111889192d90ae38a9b84704.gif)