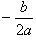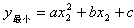同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表-数学
题文
同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
|
答案
出现“2个正面”的频率为18÷60=
“1个正面”的频率为33÷60=
“没有正面”的频率为9÷60=
同时抛掷两枚硬币,可能出现的情况为:正正,正反,反正,反反, 所以出现“2个正面”的频率为18÷60=
“1个正面”的频率为33÷60=
“没有正面”的频率为9÷60=
故答案为
|
据专家权威分析,试题“同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个..”主要考查你对 二次函数的最大值和最小值 等考点的理解。关于这些考点的“档案”如下:
二次函数的最大值和最小值
考点名称:二次函数的最大值和最小值
- 二次函数的最值:
1.如果自变量的取值范围是全体实数,则当a>0时,抛物线开口向上,有最低点,那么函数在 处取得最小值y最小值=
处取得最小值y最小值= ;
;
当a<0时,抛物线开口向下,有最高点,即当 时,函数取得最大值,y最大值=
时,函数取得最大值,y最大值= 。
。
也即是:如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当 时,
时, 。
。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:(阅读解答题)阅读下面的解题过程:妈妈给小明一串钥匙,共有4把,小明决定先试试哪把是防盗门的钥匙.如果不开门,你能说明他第一次试开就成功的概率有多大吗?写出用计算器或其-数学
下一篇:小明在游乐场看到别人正在玩一种游戏.玩一次要1元.游戏者掷两个瓶盖,若两枚瓶盖均盖面朝上则奖励5元.小明看别人玩了一会儿,并把结果记录在下表中两个都是瓶盖朝上一盖面朝-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

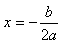
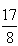
![已知(m为任意实数),则P、Q的大小关系为[]A.P>QB.P=QC.P<QD.不能确定-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/119/2019-12-17/a2d88dc8111889192d90ae38a9b84704.gif)