已知抛物线C1:,点F(1,1)。(Ⅰ)求抛物线C1的顶点坐标;(Ⅱ)①若抛物线C1与y轴的交点为A,连接AF,并延长交抛物线C1于点B,求证:;②抛物线C1上任意一点P(xp,yp)(0<xp<-九年级数学
题文
已知抛物线C1: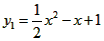 ,点F(1,1)。 ,点F(1,1)。(Ⅰ)求抛物线C1的顶点坐标; (Ⅱ)①若抛物线C1与y轴的交点为A,连接AF,并延长交抛物线C1于点B,求证: 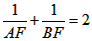 ; ; ②抛物线C1上任意一点P(xp,yp)(0<xp<1),连接PF,并延长交抛物线C1于点Q(xq,yq),试判断  是否成立?请说明理由; 是否成立?请说明理由; (Ⅲ)将抛物线C1作适当的平移,得抛物线C2:  ,若2<x≤m时,y2≤x,恒成立,求m的最大值。 ,若2<x≤m时,y2≤x,恒成立,求m的最大值。 |
答案
解 (I)∵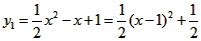 , ,∴抛物线  的顶点坐标为( 的顶点坐标为( ); ); |
||||||||||
| (II)①根据题意,可得点A(0,1), ∵F(1,1), ∴AB∥x轴, 得AF=BF=1,  ; ;② 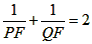 成立, 成立,理由如下: 如图,过点P( 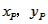 )作PM⊥AB于点M,则FM= )作PM⊥AB于点M,则FM= ,PM= ,PM=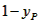 ( ( ) ) ∴Rt△PMF中,由勾股定理,得  又点P(  )在抛物线 )在抛物线 上, 上,得 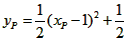 ,即 ,即 ∴  即 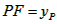 , ,过点Q( 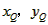 )作QN⊥B,与AB的延长线交于点N, )作QN⊥B,与AB的延长线交于点N,同理可得  , ,图文∠PMF=∠QNF=90°,∠MFP=∠NFQ, ∴△PMF∽△QNF 有 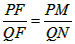 这里  , , ∴ 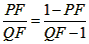 即 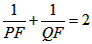 ; ; |
 | |||||||||
(Ⅲ)令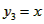 , ,设其图象与抛物线 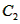 交点的横坐标为 交点的横坐标为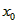 , , , ,且 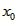 < < , , ∵抛物线 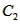 可以看作是抛物线 可以看作是抛物线 左右平移得到的, 左右平移得到的,观察图象,随着抛物线  向右不断平移, 向右不断平移, , , 的值不断增大, 的值不断增大, ∴当满足 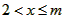 , , ,恒成立时,m的最大值在 ,恒成立时,m的最大值在 处取得, 处取得,可得当 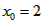 时, 时,所对应的 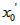 即为m的最大值, 即为m的最大值,于是,将  带入 带入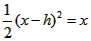 , ,有
上一篇:如图,在等腰梯形ABCD中,AD=4,BC=9,∠B=45°,动点P从点B出发沿BC向点C运动,动点Q同时以相同速度从点C出发沿CD向点D运动,其中一个动点到达端点时,另一个动点也随之停止运-九年级数学
下一篇:注意:为了使同学们更好她解答本题,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一班要求进行解答即可。某商-九年级数学
零零教育社区:论坛热帖子
|






