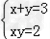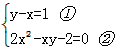周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个?-数学
题文
| 周长为6,面积为整数的直角三角形是否存在?若不存在,请给出证明;若存在,请证明共有几个? |
答案
| 设存在如上的直角三角形,设两直角边分别为a,b,斜边为c, ∵a+b+c=6(1); a2+b2=c2(2) ∴(a+b)2=(6-c)2(3) ∵
∴c为整数或以3为分母的分数; ∵直角三角形斜边最长则有c>2,根据三角形三边边长规律有c<3; ∴2<c<3; ∴c应为以3为分母的分数,c=
当c=
当c=
∴这样的直角三角形存在,恰有一个,两条直角边为
|

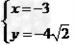
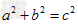
![下列方程中,有实数解的方程是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/133/2019-12-19/745552dfe644bea31ed2e3531b62441f.png)