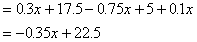题文

某农场300名职工种51公顷土地，分别种植水稻、蔬菜和棉花，种植这些农作物每亩所需工人数和预计产值如下表所示，设水稻、蔬菜和棉花的种植面积分别为x公顷、y公顷和z公顷． （1）用含x的式子表示y和z； （2）若总产值p（万元）满足：360≤p≤370，且x、y、z均为正整数，这个农场怎样安排三种农作物的种植面积才能取得最优效益？ 农作物 每公顷所需人数 每公顷预计产值 水稻 4 4.5万元 蔬菜 8 9万元 棉花 5 7.5万元

题型：解答题  难度：中档

答案

（1）依题意得 x+y+z=51        ① 4x+8y+5z=300    ② ， 由②-①×5得   3y-x=45，即y= 1 3 x+15， 由①×8-②得   4x+3z=108，即z=- 4 3 x+36； （2）∵P=4.5x+9y+7.5z=4.5x+9×( 1 3 x+15)+7.5×(- 4 3 x+36)=405-2.5x， ∴360≤405-2.5x≤370， 解之得14≤x≤18， ∵x为整数且x为3的倍数， ∴只有x=15和x=18， 当x=15时，y=20，z=16； 当x=18时，y=21，z=12， ∵y随x的增大而减小，即x越小，P越大， 所以方案一：水稻种15公顷，蔬菜种20公顷，棉花种16公顷． 方案二：水稻种18公顷，蔬菜种21公顷，棉花种12公顷． 比较选方案一为最佳． 答：（1）y= 1 3 x+15，即z=- 4 3 x+36； （2）这个农场怎样安排水稻种15公顷，蔬菜种20公顷，棉花种16公顷的种植面积才能取得最优效益．

据专家权威分析，试题“某农场300名职工种51公顷土地，分别种植水稻、蔬菜和棉花，种植这..”主要考查你对  三元（及三元以上）一次方程（组）的应用  等考点的理解。关于这些考点的“档案”如下：

三元（及三元以上）一次方程（组）的应用

考点名称：三元（及三元以上）一次方程（组）的应用

• 三元一次方程组的应用：求待定系数的值，列方程组解应用题等。