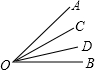
如图,0N是∠BOC的平分线,OM是∠AOC的平分线.(1)如果∠AOC=28°,∠BOC=42°,那么∠MON是多少度?(2)如果∠AOB的大小保持与上图中相同,而射线OC在∠AOB的内部绕点O转动,那么射线OM-数学
题文
| 如图,0N是∠BOC的平分线,OM是∠AOC的平分线. (1)如果∠AOC=28°,∠BOC=42°,那么∠MON是多少度? (2)如果∠AOB的大小保持与上图中相同,而射线OC在∠AOB的内部绕点O转动,那么射线OM,ON的位置是否发生变化?为什么? (3)∠MON的大小是否发生变化?如果不变,请说出其度数;如果变化,请说出变化范围.  |