题文

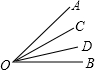
如图，已知∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC． （1）求∠MON的度数； （2）如果（1）中∠AOB=α，∠BOC=β（β为锐角），其他条件不变，求∠MON的度数； （3）从（1）、（2）的结果中能得出什么结论？ （4）线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿设计一道以线段为背景的计算题，并给出解答．

题型：解答题  难度：中档

答案

（1）∵∠AOB=90°，OM平分∠AOB， ∴∠AOM=∠BOM=45°， 同理，∠BON=∠NOC=15°， ∴∠MON=∠BOM+∠BON=45°+15°=60°． （2）∵∠AOB=α，OM平分∠AOB， ∴∠AOM=∠BOM= α 2 ， 同理，∠BON=∠NOC= β 2 ， ∴∠MON=∠BOM+∠BON= α 2 + β 2 = α+β 2 ． （3）∠MON= α+β 2 ． （4）如图示， 点D是AB的中点，点E是EC的中点，AB=8，BC=4，求DE． ∵点D是AB的中点，AB=8， ∴BD=4， 同理，BE=2， 所以DE=4+2=6．

据专家权威分析，试题“如图，已知∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC．（1）求∠M..”主要考查你对  角平分线的定义   等考点的理解。关于这些考点的“档案”如下：

角平分线的定义

考点名称：角平分线的定义

• 角的平分线的定义：
  一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

• 角平分线的性质：
  角平分线上的点，到角两边的距离相等
  定理：
  角平分线上的任意一点，到角两边的距离相等。垂直于两边为最短距离。角平分线能得到相同的两个角。三角形三条角平分线相交于一点，并且这一点到三边的距离相等。
  逆定理：
  到角两边的距离相等的点在角平分线上。