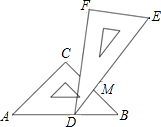
如图所示:点A和点C分别在射线BF和射线BE上运动(点A和点C不与点B重合),BF⊥BE,CD是∠ACB的平分线,AM是△ABC在顶点A处的外角平分线,AM的反向延长线与CD交于点D.试回答下列问题-数学
题文
| 如图所示:点A和点C分别在射线BF和射线BE上运动(点A和点C不与点B重合),BF⊥BE,CD是∠ACB的平分线,AM是△ABC在顶点A处的外角平分线,AM的反向延长线与CD交于点D.试回答下列问题: (1)若∠ACB=30°,则∠D=______°,若∠ACB=70°,则∠D=______° (2)设∠ACD=x,用x表示∠MAC的度数,则∠MAC=______° (3)试猜想,点A和点C在运动过程中,∠D的度数是否发生变化?若变化,请求出变化范围;若不变,请给出证明.  |