题文

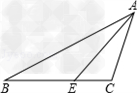
如图（甲），D是△ABC的边BC的延长线上一点．∠ABC、∠ACD的平分线相交于P1． （1）若∠ABC=80°，∠ACB=40°，则∠P1的度数为______； （2）若∠A=α，则∠P1的度数为______；（用含α的代数式表示） （3）如图（乙），∠A=α，∠ABC、∠ACD的平分线相交于P1，∠P1BC、∠P1CD的平分线相交于P2，∠P2BC、∠P2CD的平分线相交于P3依此类推，则∠Pn的度数为______（用n与α的代数式表示）

题型：解答题  难度：中档

答案

∵P1B、P1C分别平分∠ABC和∠ACD， ∴∠ACD=2∠P1CD，∠ABC=2∠P1BC， 而∠P1CD=∠P1+∠P1BC，∠ACD=∠ABC+∠A， ∴∠A=2∠P1， ∴∠P1= 1 2 ∠A， （1）∵∠ABC=80°，∠ACB=40°， ∴∠A=60°， ∴∠P1=30°； （2）∵∠A=α， ∴∠P1的度数为 1 2 α； （3）同理可得∠P1=2∠P2， 即∠A=22∠P2， ∴∠A=2n∠Pn， ∴∠Pn=（ 1 2 ）nα． 故答案为：30°， 1 2 α，（ 1 2 ）nα．

据专家权威分析，试题“如图（甲），D是△ABC的边BC的延长线上一点．∠ABC、∠ACD的平分线相交..”主要考查你对  三角形的内角和定理，三角形的外角性质，三角形的中线，角平分线，高线，垂直平分线  等考点的理解。关于这些考点的“档案”如下：

三角形的内角和定理三角形的外角性质三角形的中线，角平分线，高线，垂直平分线

考点名称：三角形的内角和定理

• 三角形的内角和定理及推论：
  三角形的内角和定理：三角形三个内角和等于180°。
  推论：
  （1）直角三角形的两个锐角互余。
  （2）三角形的一个外角等于和它不相邻的来两个内角的和。
  （3）三角形的一个外角大于任何一个和它不相邻的内角。
  注：在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角。

考点名称：三角形的外角性质

• 三角形的外角：
  三角形的一条边的延长线和另一条相邻的边组成的角，叫做三角形的外角。
  
  ∠1是三角形的外角。

• 三角形的外角特征：
  ①顶点在三角形的一个顶点上，如∠ACD的顶点C是△ABC的一个顶点；
  ②一条边是三角形的一边，如∠ACD的一条边AC正好是△ABC的一条边；
  ③另一条边是三角形某条边的延长线如∠ACD的边CD是△ABC的BC边的延长线。
   
  性质：
  ①. 三角形的外角与它相邻的内角互补。
  ②. 三角形的一个外角等于和它不相邻的两个内角的和。
  ③. 三角形的一个外角大于任何一个和它不相邻的内角。
  ④. 三角形的外角和等于360°。
  设三角形ABC 则三个外角和=（A+B）+（A+C）+（B+C）=360度。
  
  定理：三角形的一个外角等于不相邻的两个内角和。
  定理：三角形的三个内角和为180度。

考点名称：三角形的中线，角平分线，高线，垂直平分线

• 三角形的中线：
  在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线。由于三角形有三条边，所以一个三角形有三条中线。且三条中线交于一点。这点称为三角形的重心。
  每条三角形中线分得的两个三角形面积相等。
  角平分线：
  三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线。
  三角形的角平分线不是角的平分线，是线段。角的平分线是射线。
  高线：
  从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）。
  线段的垂直平分线：
  经过某一条线段的中点，并且垂直于这条线段的直线，叫做这条线段的垂直平分线。
  

  <?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />注意：要证明一条线为一个线段的垂直平分线，应证明两个点到这条线段的距离相等且这两个点都在要求证的直线上才可以证明
  巧计方法：点到线段两端距离相等。

• 三角形中线性质定理：
  1、三角形的三条中线都在三角形内。<?xml:namespace prefix = "o" ns = "urn:schemas-microsoft-com:office:office" />

  2、三角形的三条中线长：

  ma=(1/2)√2b²+2c² -a² ；

  mb=(1/2)√2c²