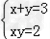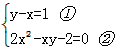(1)求满足y4+2x4+1=4x2y的所有整数对(x,y);(2)求出所有满足5(xy+yz+zx)=4xyz的正整数解.-数学
题文
| (1)求满足y4+2x4+1=4x2y的所有整数对(x,y); (2)求出所有满足5(xy+yz+zx)=4xyz的正整数解. |
答案
| (1)∵y4+2x4+1=4x2y?(2x4-4x2y+2y2)+(y4-2y2+1)=0?2(x2-y)2+(y2-1)2=0, ∴x2-y=0,y2-1=0, ∴原方程的所有整数解为(1,1)、(-1,1); (2)∵5(xy+yz+zx)=4xyz?
∵4/5=(1/5)+(3/5)=(1/5)+(6/10)=(1/5)+(1/10)+(5/10)=(1/2)+(1/5)+(1/10). ?x,y,z的值循环为2,5,10, ∵
|

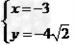
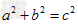
![下列方程中,有实数解的方程是[]A.B.C.D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/133/2019-12-19/745552dfe644bea31ed2e3531b62441f.png)