题文

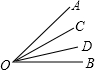
如图，BD是∠ABC的平分线，ED∥BC，∠FED=∠BDE，则EF也是∠AED的平分线．完成下列推理过程： 证明：∵BD是∠ABC的平分线（______） ∴∠ABD=∠DBC（______） ∵ED∥BC（______） ∴∠BDE=∠DBC（______） ∴______（______） 又∵∠FED=∠BDE（______） ∴______∥______（______） ∴∠AEF=∠ABD（______） ∴∠AEF=∠DEF（______） ∴EF是∠AED的平分线（______）

题型：解答题  难度：中档

答案

证明：∵BD是∠ABC的平分线（已知）， ∴∠ABD=∠DBC（角平分线定义）； ∵ED∥BC（已知）， ∴∠BDE=∠DBC（两直线平行，内错角相等）， ∴∠ABD=∠BDE（等量代换）； 又∵∠FED=∠BDE（已知）， ∴EF∥BD（内错角相等，两直线平行）， ∴∠AEF=∠ABD（两直线平行，同位角相等）， ∴∠AEF=∠DEF（等量代换）， ∴EF是∠AED的平分线（角平分线定义）．

据专家权威分析，试题“如图，BD是∠ABC的平分线，ED∥BC，∠FED=∠BDE，则EF也是∠AED的平分..”主要考查你对  角平分线的定义   等考点的理解。关于这些考点的“档案”如下：

角平分线的定义

考点名称：角平分线的定义

• 角的平分线的定义：
  一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

• 角平分线的性质：
  角平分线上的点，到角两边的距离相等
  定理：
  角平分线上的任意一点，到角两边的距离相等。垂直于两边为最短距离。角平分线能得到相同的两个角。三角形三条角平分线相交于一点，并且这一点到三边的距离相等。
  逆定理：
  到角两边的距离相等的点在角平分线上。