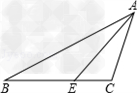
阅读下题并填空:已知:△ABC,∠A、∠B、∠C之和为多少?为什么?∠A+∠B+∠C=180°理由:作∠ACD=∠A,并延长BC到E∵∠1=∠A(已作)∴AB∥CD(______)∴∠B=______(______)而∠ACB+∠1+∠2=180°∴∠ACB+-数学
题文
| 阅读下题并填空: 已知:△ABC,∠A、∠B、∠C之和为多少?为什么? ∠A+∠B+∠C=180° 理由:作∠ACD=∠A,并延长BC到E ∵∠1=∠A(已作) ∴AB∥CD(______) ∴∠B=______(______) 而∠ACB+∠1+∠2=180° ∴∠ACB+______+______=180°(等量代换)  |